Vysoké učení technické v Brně
Fakulta stavební
Ústav stavební mechaniky
Diplomová práce
Práce vznikla jako součást výzkumného záměru fakulty reg. č. CEZ:J22/98:2261100009

Diplomant: Petr Frantík
Vedoucí diplomové práce: Ing. Zbyněk Keršner, CSc., doc. RNDr. Jiří Macur, CSc., Ing. Jiří Vrba
Brno, květen 2000
Poděkování
Děkuji všem mým vedoucím diplomové práce za pomoc, vedení a připomínky, které mi umožnily vypracování této práce.
Prohlášení
Prohlašuji, že předloženou diplomovou práci jsem vypracoval samostatně, s použitím uvedených zdrojů informací.
Petr Frantík
OBSAH
Předmětem této práce je studium modelu jednostranně vetknutého nosníku - konzoly. Model je zjednodušený a závislý na času (nazývá se dynamický), nelineární a je vyšetřován v rozsahu malých i velkých deformací. Účelem je zjistit, zdali i takový model, nutně jednodušší než skutečnost a zbavený vnější nahodilosti, může vykazovat nepredikovatelné chování.
Největším problémem a zároveň nejzodpovědnějším úkolem je tedy věrně modelovat skutečnou konstrukci tak, aby získané výsledky měly pro reálnou představu smysl. Intuitivně lze předpokládat, že pokud bude takový model od určitých mezí vykazovat nepredikovatelné chování, potom i u skutečné konstrukce mohou existovat meze, za kterými nebude jednoduchá souvislost mezi dějem na konstrukci a jejím chováním.
Vzhledem k trendu používání rozmanitých materiálů, k navrhování materiálově úspornějších konstrukcí, k čím dál větší odvaze projektantů a neustále se rozšiřujícím možnostem výpočetní techniky, lze očekávat rozšiřující se požadavky na vyšetřování nelineárního chování konstrukcí. Tato práce se má tedy o řešení takového problému pokusit.
Téma práce bylo vybráno jako krok do prostředí nových věd, které nejsou, nebo teprve začínají být aplikovány ve stavební mechanice. Tyto vědní obory se nazývají teorie dynamických systémů a teorie chaosu. V práci však využívám pouze některé z nástrojů, které si tyto vědní obory vzaly za své. Lze říci, že se práce zabývá pouze simulací nelineárního dynamického systému a je tedy prací experimentální. Matematicky půjde o diskrétní numerické řešení počátečního problému nehomogenní nelineární diferenciální rovnice druhého řádu (rozložené na soustavu dif. rovnic prvního řádu). Z hlediska stavební mechaniky je to konzola jako tlumený oscilátor s jedním stupněm volnosti s uvažováním fyzikální a geometrické nelinearity, zatížená konzervativní harmonickou budící silou (bylo zachováno maximum použitelných zjednodušení).
V literatuře (např. [2]), kterou jsem měl k dispozici, jsem našel modely, kterým chyběla použitelnost pro vybranou konstrukci vzhledem k chybějící geometrické nelinearitě při velkých deformacích.
Zjistil jsem, že je-li fyzikální nelinearita významná a jsou-li výchylky velké, je přítomnost nepředpovídatelného chování možná. Avšak zkoumaný systém, jak bude dále ukázáno, se choval velmi stabilně.
Stavová proměnná
Za dynamický systém budeme považovat systém, který je popsán konečnou množinou stavových proměnných. Stavové proměnné jsou vybrané fyzikální veličiny, které svou proměnlivostí v čase jednoznačně popisují vývoj systému. To znamená, že okamžitý stav systému plně určuje jeho vývoj. V tomto případě budou stavové proměnné úhlová výchylka  , úhlová rychlost
, úhlová rychlost 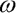 a fáze budící síly
a fáze budící síly 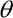 .
.
 | Model konstrukce se znázorněnými stavovými proměnnými. Úhlová výchylka  měřená od horizontální osy (stavu, kdy je konstrukce nezatížená), úhlová rychlost měřená od horizontální osy (stavu, kdy je konstrukce nezatížená), úhlová rychlost 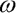 , jejíž funkce je derivací funkce úhlové výchylky. Fáze budící síly , jejíž funkce je derivací funkce úhlové výchylky. Fáze budící síly 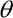 . .
|
Fázový prostor
Hodnoty stavových proměnných lze zobrazit bodem ve fázovém prostoru. Fázový prostor je lineární prostor, jehož každý rozměr reprezentuje stavovou proměnnou systému. Má tedy tolik rozměrů, kolik má daný systém stavových proměnných.
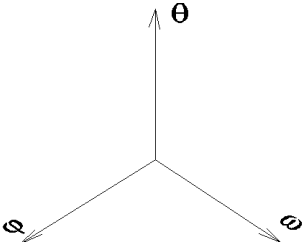
Obr.: Souřadná soustava trojrozměrného fázového prostoru vybraného dynamického systému.
Definice dynamického systému (převzato z [1])
Je-li x uspořádaná množina (vektor) stavových proměnných ve fázovém prostoru R(n): (x1, x2, ..., xn) nazveme modelem dynamického systému soustavu diferenciálních rovnic:
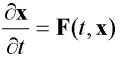
kde t je čas a F je vektorová funkce, tj. po rozepsání

Uvedenou soustavu lze vytvořit i ze soustavy diferenciálních rovnic vyšších řádů jednoduchou substitucí (viz část Simulace/Diferenciální rovnice).
Trajektorie systému (převzato z [1])
Řešením soustavy je vektor funkcí x(t)=(x1(t), x2(t), ... , xn(t)).
Vývoj systému lze pak znázornit parametrickou křivkou x(t) ve fázovém prostoru, kterou nazýváme trajektorií systému. Trajektorie systému je množina bodů ve fázovém prostoru, kterými daný systém v čase prochází. Pro každý bod ve fázovém prostoru existuje pouze jedna trajektorie. Z toho plyne, že se trajektorie nemohou protínat, protože by nebylo možno rozhodnout, jak se má systém dále vyvíjet.
 | Anaglyfové znázornění části trajektorie dynamického systému se třemi stavovými proměnnými. Anaglyf je označení pro dva či více horizontálně uspořádaných obrázků, sloužících pro vyvolání trojrozměrnosti zobrazeného objektu. Na anaglyf je třeba dívat se tak, že levé oko sleduje levou část ze dvojice a pravé oko pravou část. V mozku se tak vytvoří průsečný objekt, který je trojrozměrný. |
Parametry systému
V diferenciálních rovnicích jsou obecně přítomny kromě stavových proměnných a času také parametry systému. Parametr systému je fyzikální veličina, která určuje proporce modelu. Parametry mohou být konstantní, nebo se mohou v čase měnit.
 | Znázornění parametrů systému. Jednotlivými parametry jsou: hmotnost hmotného bodu m, délka závěsu L, konstanta útlumu c, gravitační zrychlení g, nelineární součinitel  , lineární tuhost s, amplituda budící síly A, frekvence budící síly , lineární tuhost s, amplituda budící síly A, frekvence budící síly  . . |
Počáteční podmínky
Každý fyzikální děj musí začít počátečními podmínkami (musí existovat stav, který budeme brát jako počátek). V modelu jsou těmito podmínkami počáteční hodnoty stavových proměnných.
Chaotické chování
S počátečními podmínkami souvisí i predikovatelnost chování systému. Lze říci, že známe-li přesně počáteční podmínky (což není ve skutečnosti možné) a známe-li přesně zákony, jimiž se systém řídí, dokážeme libovolně dlouho přesně předpovídat budoucí chování systému [4]. V případě, že je přesně neznáme, vzniká problém, jaký vliv bude mít nepřesnost v těchto podmínkách na přesnost předpovědi. Potom tedy chaotickým chováním systému nazveme takové chování, při kterém je systém citlivý na počáteční podmínky. Jinými slovy je nestabilní a nepredikovatelný. Libovolně malá chyba způsobí v konečném čase odlišné chování.
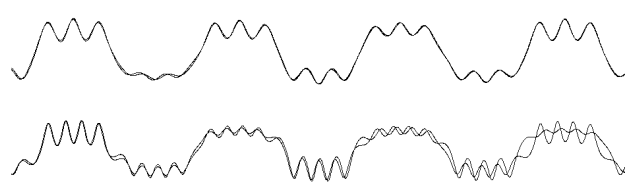
Obr.: Znázornění vlivu počátečních podmínek. V horní i dolní části je dvojice trajektorií pro mírně odlišné počáteční podmínky. Horní dvojice je stabilním chováním, je patrno že odlišnost počátečních podmínek nemá velký vliv. U dolní dvojice je v pravé části patrno, že rozdíl v počátečních podmínkách způsobil výrazně odlišnou odezvu systému. Zcela zřejmě tedy jde o nestabilní chování.
Fraktál
Důsledkem nelinearity systému mohou při určitém grafickém zobrazení vznikat různé geometrické útvary, které jsou měřítkově soběpodobné [6]. To jednoduše znamená, že zvětšováním útvaru se neztrácí jeho složitost, neustále nacházíme podobné tvary či seskupení v různých měřítkách. Takový útvar nazýváme fraktál (více informací o fraktálech ve stavebnictví viz např. Petr Cacka, Fraktální vlastnosti lomových ploch cementových kompozitů). Fraktální složitost je typickým projevem nelineárních systémů.

Obr.: Obrázek dvou fraktálů. Levý fraktál se nazývá dračí křivka a pravý C křivka. Oba vznikají jednoduchým iteračním výpočtem, kdy se nad odvěsnami pravoúhlého rovnoramenného trojúhelníka konstruují nové trojúhelníky stejného druhu, ovšem jejich přepony jsou odvěsnami původního trojúhelníka. Rozdíl obou fraktálů je dán polohou vytváření nových trojúhelníků. Z obrázku je patrno, že jednotlivé útvary se skládají ze zmenšených obdob těchto útvarů.
Jestliže je dynamický systém systémem, kde se energie ztrácí (nazývá se disipativní), dochází v čase k přibližování trajektorie k určité množině bodů ve fázovém prostoru. Tato množina se pro čas jdoucí do nekonečna nazývá limitní množinou. Je-li taková množina bodem, nazývá se limitní bod. Je-li takovou množinou uzavřená křivka (orbit), nazývá se limitní cyklus. Není-li množina kompaktní, nazývá se podivný atraktor, který je výsledkem chaotického chování.
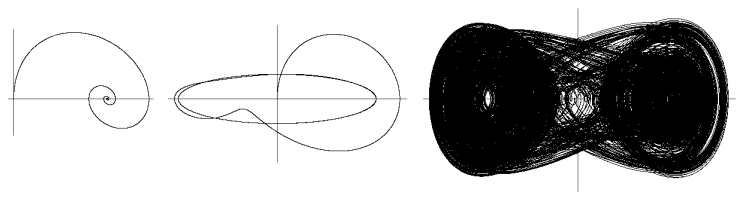
Obr.: Trojice projekcí trajektorie do roviny. Jednotlivé projekce ukazují, do jakého limitního cyklu systém dospěl. V levém případě je patrné přibližování se k limitnímu bodu. Uprostřed je limitním cyklem elipsa a vpravo je projekcí nepříliš názorně zobrazen podivný atraktor
Zobrazení vývoje systému je klíčové pro jeho zkoumání a proto si jej rozdělíme.
Závislost stavové proměnné na času
Průběh stavových proměnných lze zobrazit jako graf závislosti vybrané stavové proměnné na času. Může sloužit jako srovnání průběhů různých řešení, nebo jako zdroj nahrazení spojitými aproximacemi funkcí. V našem případě může sloužit k poznání souvislostí mezi stavovou proměnnou a funkcí budící síly.
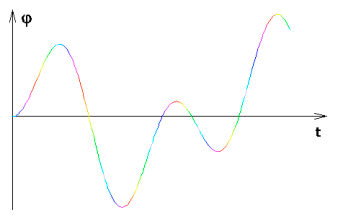 | První z trojice po sobě jdoucích obrázků, vysvětlující vliv použitého zobrazení na porozumění chování systému. Je znázorněním závislosti stavové proměnné  na čase t. na čase t. |
Závislost energií systému na času
Průběh kinetické, potenciální a celkové energie systému v závislosti na času může sloužit jako ukazatel stability numerického řešení i jako ukazatel chaotického chování.
Trajektorie systému a její projekce
Je základním zobrazením vývoje systému. Lze použít k nalezení limitních množin systému, k testu numerické stability a k hledání souvislostí mezi jednotlivými stavovými proměnnými.
 | Druhý z obrázků. Anaglyf téže trajektorie. Oproti předchozímu obrázku přibývají stavové proměnné 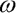 a a 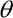 . Časová osa se ztratila. Je však stále nepřímo přítomna jako lineární transformace osy stavové proměnné . Časová osa se ztratila. Je však stále nepřímo přítomna jako lineární transformace osy stavové proměnné 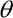 . Předchozí obrázek je vlastně lineárně transformovanou projekcí této trajektorie do roviny . Předchozí obrázek je vlastně lineárně transformovanou projekcí této trajektorie do roviny  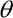 . . |
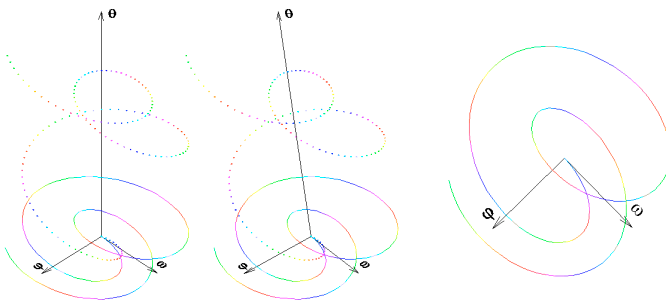
Obr.: Třetí z obrázků. Opět tentýž systém, ale tentokrát v projekci do roviny 
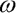 kolmé na osu stavové proměnné
kolmé na osu stavové proměnné 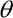 . V levé části je anaglyfové zobrazení ztráty jedné dimenze při použití projekce (body označují původní trajektorii, projekce trajektorie je patrná v podstavné rovině
. V levé části je anaglyfové zobrazení ztráty jedné dimenze při použití projekce (body označují původní trajektorii, projekce trajektorie je patrná v podstavné rovině 
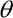 ). V pravé části je výsledná projekce.
). V pravé části je výsledná projekce.
Fázový portrét systému
Slouží k zobrazení závislosti tvaru a polohy trajektorie na počátečních podmínkách. Použitelný u systémů se dvěmi stavovými proměnnými.
Závislost polohy a tvaru limitní množiny na počátečních podmínkách
Použije se, když existuje více limitních množin. Slouží k nalezení míst, jež jsou problematická pro určení výsledné limitní množiny. Nazývá se též oblasti či bazény přitažlivosti.
V našem případě budou proměnlivými počátečními podmínkami počáteční úhlová výchylka
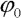 a počáteční úhlová rychlost
a počáteční úhlová rychlost 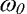 . Tato dvojice tedy vytváří rovinu možných počátečních podmínek. Z této roviny budeme vybírat body a zjišťovat do jakého limitního cyklu systém dospěje. Bod potom zobrazíme pod barvou, příslušnou k právě onomu limitnímu cyklu.
. Tato dvojice tedy vytváří rovinu možných počátečních podmínek. Z této roviny budeme vybírat body a zjišťovat do jakého limitního cyklu systém dospěje. Bod potom zobrazíme pod barvou, příslušnou k právě onomu limitnímu cyklu.
Řez trajektorií systému
Slouží k zobrazení vývoje či tvaru limitní množiny systému s více stavovými proměnnými (nazývá se též Poincarého mapa). Vhodný pro detekci chaotického chování a pro stanovení zlomkové (fraktální) dimenze limitní množiny a pro detailní studium podivných atraktorů.
V našem případě trajektorie systému není uzavřena v prostorově omezeném útvaru a její řez rovinou je buď pouhým bodem, nebo s časem se rozšiřující skupinou bodů. Proto nepovedeme řez jednoduchou rovinou, ale periodicky se opakující rovinou. Rovina bude vždy kolmá na stavovou proměnnou fáze budící síly. Perioda opakování řezu bude 2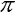 .
.
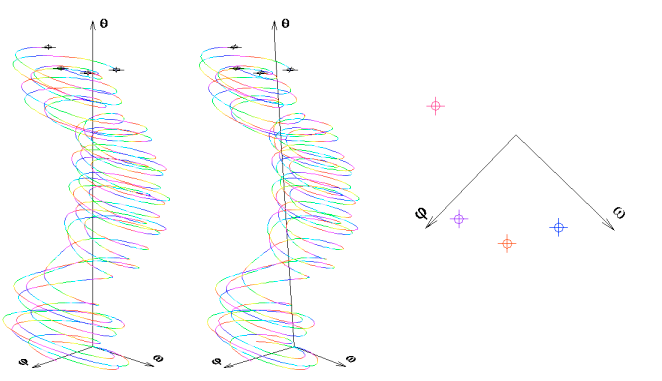
Obr.: Vytváření řezu trajektorie. Na obrázku je praktické znázornění periodicky se opakujícího řezu. Trajektorie rozvíjející se ve skutečnosti ve směru dimenze 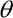 do nekonečna je rozdělena řezy na části a ty jsou posunuty do intervalu mezi počátkem a prvním řezem. Vzniká tedy prostorově omezený útvar, který je informačně stejně hodnotný (žádná informace se posuny neztrácí). Pro vynesení řezu se zobrazí vždy bod průniku trajektorie řeznou rovinou, jak je zobrazeno na anaglyfu v horních částech trajektorií pomocí kolečka s křížkem. V pravé části je vidět výsledný řez (jedná se o ilustrativní příklad, při skutečné simulaci může být bodů v řezu nesrovnatelně větší počet).
do nekonečna je rozdělena řezy na části a ty jsou posunuty do intervalu mezi počátkem a prvním řezem. Vzniká tedy prostorově omezený útvar, který je informačně stejně hodnotný (žádná informace se posuny neztrácí). Pro vynesení řezu se zobrazí vždy bod průniku trajektorie řeznou rovinou, jak je zobrazeno na anaglyfu v horních částech trajektorií pomocí kolečka s křížkem. V pravé části je vidět výsledný řez (jedná se o ilustrativní příklad, při skutečné simulaci může být bodů v řezu nesrovnatelně větší počet).
Závislost stavové proměnné nebo stavové proměnné v řezu limitní množiny na vybraném parametru
Slouží jako nástroj pro mapování oblastí chaotického chování a pro identifikaci význačných hodnot parametru. Nazývá se též dle svého tvaru bifurkační diagram.
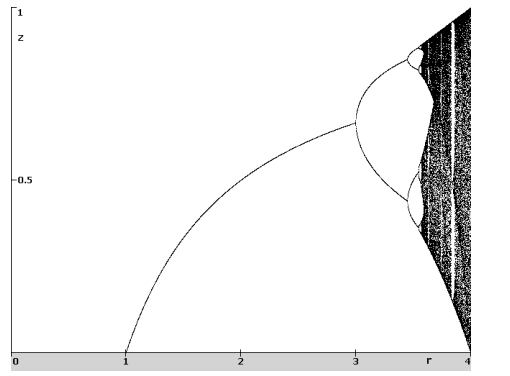 | Bifurkační diagram diskrétního systému, používaného v biologii [3]. Je tvořen jednoduchou iterační rovnicí zi+1=zir(1-zi). Kde r je parametr nazvaný růstový faktor a z je stavová proměnná nazvaná populace. Pro zvolený růstový faktor je pro nějakou počáteční hodnotu populace z intervalu (0;1) proveden iterační proces. Je-li tento proces ukončen, vynese se několik po sobě jdoucích populací do grafu. Z grafu je zřejmé, že pro hodnotu r v intervalu (1;3) se systém ustálil do jediné hodnoty populace. Při hodnotě tři začnou populace oscilovat mezi dvěmi hodnotami. Dojde k rozdvojení (bifurkaci). Za určitou mezí se u systému nedá říci, že by se ustálil do konečného počtu populací. Dostáváme se do oblasti chaotického chování. Avšak i dále se dají nalézt stabilní oblasti, v nichž systém není chaotický. |
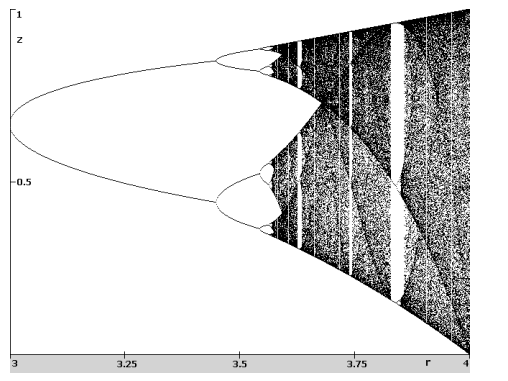 | Zvětšení části bifurkačního diagramu z předchozího obrázku. Jsou zde vidět stabilní oblasti střídající se s oblastmi chaosu. Také je z obrázku patrno, že v oblastech chaotického chování existuje jistý řád. Populace se soustředí kolem určitých hodnot. |
Závislost extrémů stavové proměnné na vybraném parametru
Slouží pro stanovení význačných hodnot parametru (například funkce frekvenční odezvy).
V našem případě mají extrémy výchylky zásadní význam. Pomocí nich se dá přibližně určit extrémní napjatost v konstrukci. Výsledků lze použít pro posouzení konstrukce v závislostech na změnách parametrů.
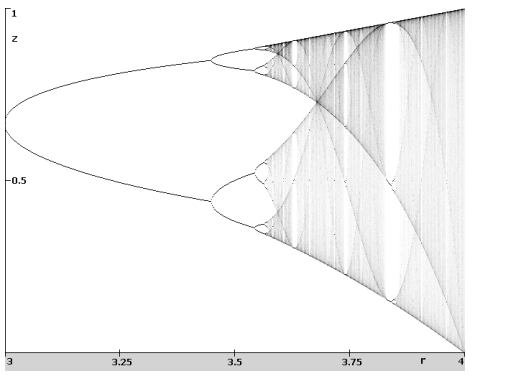
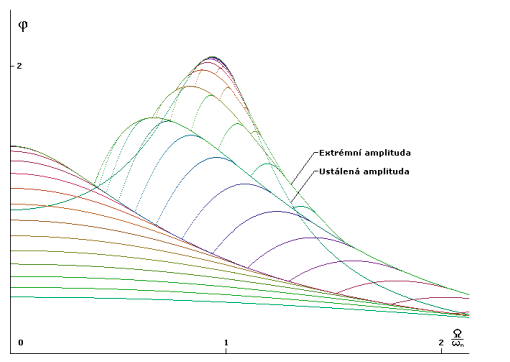 | Průběh aproximací funkce frekvenční odezvy lineárního tlumeného oscilátoru s koeficientem poměrného útlumu 0.25. Počáteční podmínky jsou nulové a budící funkce je kosinová. Barvy jsou použity pro rozlišení jednotlivých aproximací. Na obrázku jsou dvě výsledné křivky. Křivka extrémní amplitudy, tvořená nejpřesnější aproximací a křivka ustálené amplitudy, která je vykreslena na základě odvozeného vztahu. Z obrázku je dobře patrno, že nejvíce iterací si vyžádá oblast rezonance. Také lze rozpoznat, že vrchol rezonance je vlivem tlumení posunut od hodnoty jedna vlevo. Z obrázku lze vyvodit jednoduchý závěr, že pro nižší napjatost pružiny oscilátoru je výhodnější budící frekvence  větší než vlastní frekvence oscilátoru větší než vlastní frekvence oscilátoru 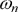 . . |
Zobrazení četnosti výskytu trajektorií v histogramu
Slouží pro lepší znázornění limitní množiny v chaotickém režimu. Ukazuje, kterými částmi limitní množiny trajektorie prochází častěji, jinak řečeno které části jsou více přitažlivé.
 | Obrázek znázorňující bifurkační diagram v histogramové podobě. Jednotlivým hodnotám populace je přiřazen odstín šedé. Čím tmavší je tento odstín, tím je hodnota populace četnější. Z obrázku je mnohem lépe vidět vnitřní struktura diagramu, nejčastější hodnoty populace vytvářejí v chaotickém režimu spojité křivky. |
Metody řešení soustavy diferenciálních rovnic
Pro simulaci systému, vzhledem k jeho neřešitelnosti analytickými postupy (zjednodušující metody analytického řešení nepřichází vzhledem ke svým zjednodušením v úvahu), využijeme diferenčních explicitních numerických metod aplikované matematiky. Numerické metody, které použijeme, nahrazují spojité řešení
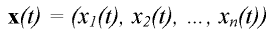
posloupností diskrétních bodů
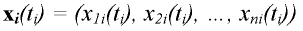
kde ti je tzv. uzel sítě pro nějž platí ti < ti + 1, n je počet stavových proměnných a i = 0, 1, 2, ….
Vzdálenost hi = ti + 1 - ti se nazývá krok metody. Pokud je hi stejné pro všechna i (je konstantní), nazývá se takové dělení sítě ekvidistantní. V našem případě použijeme ekvidistantní dělení, proto označíme h = hi.
Eulerova metoda
Pro i-tou stavovou proměnnou v čase tn + 1 platí:
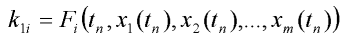
Klasická Runge-Kuttova metoda
Pro i-tou stavovou proměnnou v čase tn + 1 platí:


Tato práce má ukázat, že i jednoduchá konstrukce se může chovat nepredikovatelně. Proto byla vybrána konzola ve své zřejmě nejjednodušší podobě. Na volném konci pružně vetknutého, neohebného, nehmotného a neprodloužitelného prutu se soustředí hmota ve hmotném bodu. Požadavek je to sice nesplnitelný, ale vzhledem k tomu, že nás bude zajímat pouze pohyb koncového hmotného bodu, je toto zjednodušení vhodné.
Reálné konstrukce stavební mechaniky se chovají tak, že po odstranění vlivu, který způsobí jejich rozkmitání, dojde k postupnému uklidnění. Pohyb se zastaví. Tomuto jevu říkáme útlum. Je to důsledkem toho, že energie, kterou má pohybující se konstrukce, je přeměňována na tepelnou energii, na zrychlení pohybu molekul vzduchu, na materiálové přeměny, aj. Modelovým systémům, kde se energie ztrácí, říkáme disipativní. Je to vlastně důsledek toho, že jsme do systému přímo nezahrnuli všechno, co s jeho chováním souvisí. Jinak řečeno, určité vnější jevy jsme abstrahovali (myšlenkově převedli) jako vnitřní vlastnost systému. Vzhledem k této úvaze se tedy ve skutečnosti v úplných systémech energie neztrácí. Jestliže takový systém, ve kterém se energie neztrácí, modelujeme, říkáme mu konzervativní.
Protože chceme získat představu o nelineárním dynamickém chování, vytvoříme model nelineární. Připustíme-li velké deformace modelu, tak abychom nemohli zanedbat jejich vliv, vznikne nelineární člen zohledňující geometrický stav. Tento člen nazveme nelinearitou geometrickou. Druhý nelineární člen se bude nacházet ve funkci napjatosti pružiny, jinak řečeno závislosti momentu v pružném vetknutí na pootočení prutu. Tento člen, vyjadřující fyzikální vlastnost pružiny, nazveme nelinearitou fyzikální.
Abychom mohli systém studovat, musíme do něj vložit energii. Protože náš systém bude tlumený, bude vhodné zajistit, aby energie byla do systému přiváděna neustále. Proto necháme na systém působit v čase proměnlivou parametrizovanou budící sílu.
Funkce momentu
Funkce napjatosti pružiny (momentu ve vetknutí), musí splňovat určité požadavky. Měla by být jednoduchá, být středově symetrická k počátku a v oblasti malých deformací by měla mít téměř lineární průběh [5]. Tyto požadavky splňuje neúplný kubický polynom s lineárním a kubickým členem.
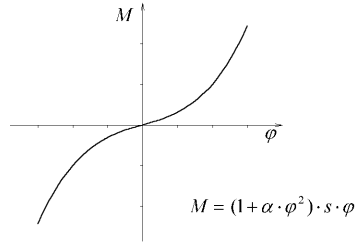
Obr.: Ilustrativní obrázek průběhu funkce momentu ve vetknutí.
Vyjmenujeme si všechny síly, které působí na hmotný bod, jehož pohyb je středem našeho zájmu:
Setrvačná síla
Je silou, která působí vždy proti směru zrychlení pohybu. Je přímo úměrná součinu hmotnosti zrychlující hmoty a zrychlení této hmoty. V našem případě:

kde m je hmotnost hmotného bodu a a je jeho obvodové zrychlení.
Gravitační síla
V důsledku trvalého gravitačního zrychlení vzniká síla, působící proti směru gravitačního zrychlení. Protože gravitační zrychlení není závislé na poloze hmotného bodu, působí síla svisle. Je přímo úměrná součinu gravitačního zrychlení a hmotnosti zrychlující hmoty. V našem případě:

kde m je hmotnost hmotného bodu a g je gravitační zrychlení.
Gravitační síla je jedinou z působících sil, která nepůsobí v závislosti na výchylce prutu. Způsobuje, že se systém projevuje nesymetricky.
Vratná síla
V pružném vetknutí závěsného prutu je přítomna pružina s nelineární závislostí síly v této pružině na úhlové výchylce pružiny (zvolili jsme neúplný kubický polynom). Tento účinek se dá nahradit silou kolmou k závěsnému prutu, působící na hmotný bod směrem zpět ke klidovému stavu systému:
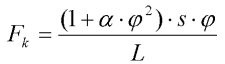
kde  je úhlová výchylka hmotného bodu vzhledem ke středu otáčení,
je úhlová výchylka hmotného bodu vzhledem ke středu otáčení,  je parametr nelinearity a s je lineární tuhost pružiny.
je parametr nelinearity a s je lineární tuhost pružiny.
Tlumící síla
Jako tlumení zvolíme nejjednodušší případ, kdy je tlumící síla přímo úměrná obvodové rychlosti hmotného bodu a působí proti směru pohybu:
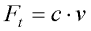
kde c je parametr útlumu a v je obvodová rychlost hmotného bodu.
Budící síla
Je to síla, která je společně s gravitační silou jednoznačně vnějším zatížením. U skutečných úloh se setkáváme s mnoha druhy vnějších sil, které mají různou velikost a různý průběh velikosti v čase. Soustředíme se proto jen na zvláštní případ, kterým je harmonická síla. Její časový průběh je kosinová funkce. V našem případě ji necháme působit vždy svisle:
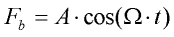
kde A je amplituda (maximální velikost síly),  je frekvence a t je čas.
je frekvence a t je čas.
Pro sestavení pohybové rovnice použijeme momentovou podmínku ke středu otáčení (bodu vetknutí). Aby byla konstrukce v dynamické rovnováze, musí v každém časovém okamžiku platit, že součet všech momentů působících sil je roven nule.
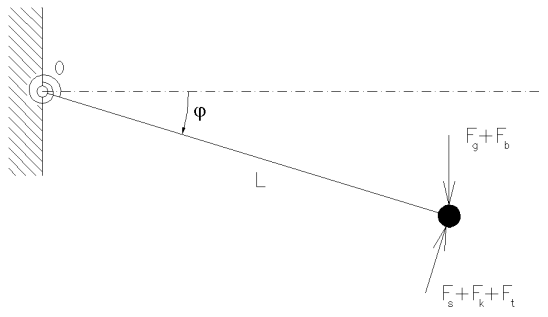
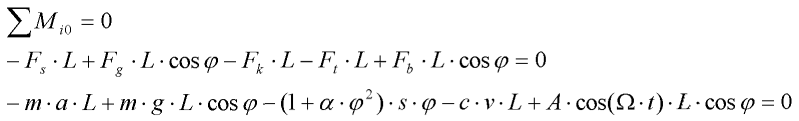
Obvodové zrychlení a a obvodovou rychlost v nahradíme:
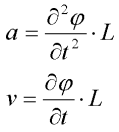
Po dosazení přejde rovnice na tvar:
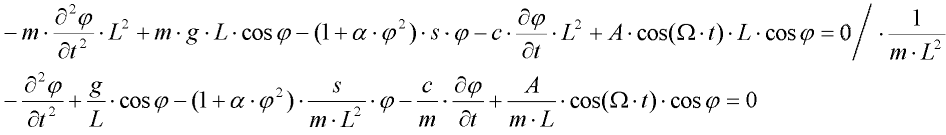
Vytkneme člen cos a uspořádáme rovnici podle derivací:
a uspořádáme rovnici podle derivací:

Substituce
Pro zkrácení zápisu diferenciální rovnice, nahradíme koeficienty jednotlivých členů novými:
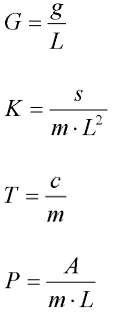
Potom rovnice přejde na tvar:
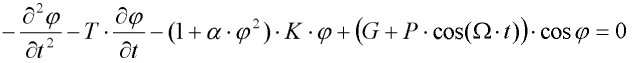
Kde  .
.  3 . K je nelineární člen nazvaný fyzikální nelinearita a závislost na cos
3 . K je nelineární člen nazvaný fyzikální nelinearita a závislost na cos  je geometrická nelinearita.
je geometrická nelinearita.
Dynamický systém
Abychom mohli pro řešení diferenciální rovnice použít numerické metody, musíme ji upravit na tvar definovaný jako dynamický systém (část Nástroje/Dynamický systém).
První stavovou proměnnou bude úhlová výchylka  . Další stavové proměnné budou úhlová rychlost
. Další stavové proměnné budou úhlová rychlost 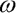 a fáze budící síly
a fáze budící síly 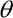 , které definujeme takto:
, které definujeme takto:
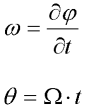
Potom lze rovnici přepsat na soustavu tří diferenciálních rovnic prvního řádu, což je náš hledaný dynamický systém:
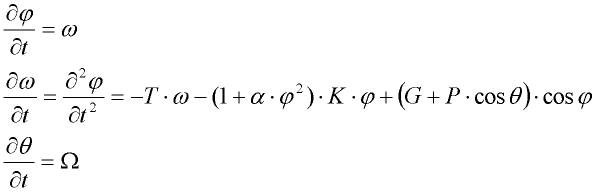
Tento tvar zápisu dynamického systému lze nazvat kanonickým zápisem soustavy diferenciálních rovnic prvního řádu. U každé z rovnic soustavy je na levé straně derivace jedné ze stavových proměnných, jejichž hodnoty budeme hledat.
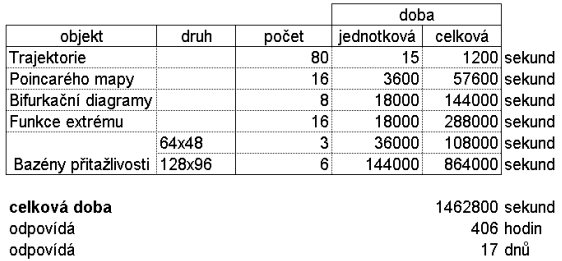
Prostorem, kde budeme provádět vlastní simulaci, bude počítač. Proto jsem musel zvolit vhodné zařízení, programovací jazyk a jeho překladač, resp. kompilátor. K dispozici jsem měl počítače palmtop Psion Series 3a 9 MHz a PC AMD K6 300 MHz, programovací jazyky OPL (Psion), Pascal, AutoLISP, C++ (PC), s odpovídajícími překladači, resp. kompilátory (přehled o výpočetním výkonu v příloze).
Jako zařízení bylo zvoleno PC a pro jazyk hlavního zdrojového kódu byl zvolen Pascal. Nicméně obě zařízení i všechny programovací jazyky byly pro zpracovávání využity (seznam souborů zdrojových kódů v příloze).
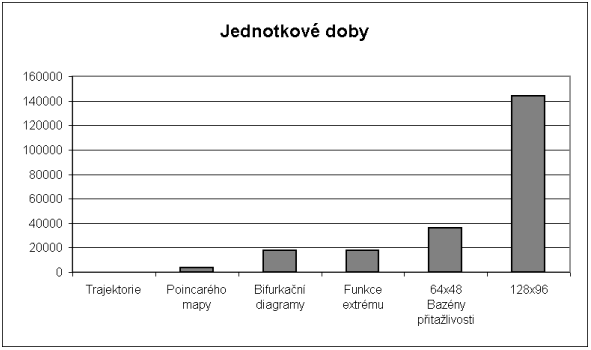
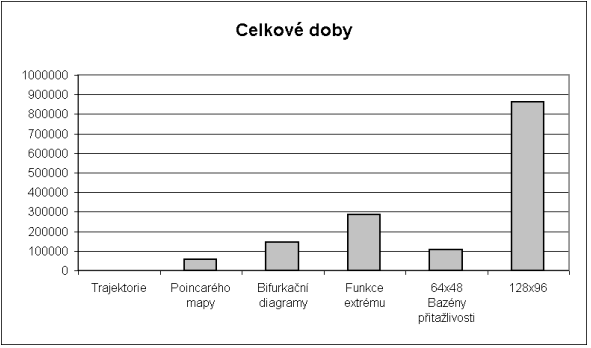
Odhad využitého čistého výpočetního času pro simulace zvoleného dynamického systému v rámci práce je 17 dnů (přehled v příloze).
Již v předchozí části byly vyjmenovány parametry, jejichž velikosti musí být nějakým způsobem určeny.
 [-]
[-] [rad.s-1]
[rad.s-1]Poslední dva parametry, amplituda a frekvence budící síly, jsou volné. V závislosti na jejich změně a na změně parametru budeme zkoumat vlastnosti našeho systému. Ostatní parametry, vyjma gravitačního zrychlení, musíme tedy zvolit.
Daný parametr
Měření na skutečné konstrukci
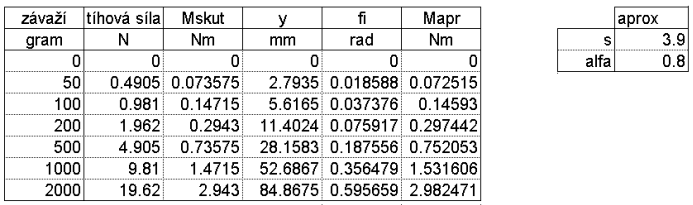
V období, kdy jsem sestavoval diferenciální rovnici jsme v předmětu mechanika materiálu prováděli zatěžovací zkoušku konzoly z pružinové oceli. Protože jsme konzolu zatěžovali i v oblasti velkých deformací, mohl jsem použít tuto konzolu i výsledky měření v této práci (měření a vyhodnocení v příloze). Tyto parametry byly vztaženy ke zkoušené konzole:
 = 0.8
= 0.8
Volený parametr
Parametr útlumu jsem neměl možnost změřit a proto jsem jej zvolil. Zvolená hodnota je poměrně nízká:
Volně závislý parametr
Nelineární součinitel  je parametr, jehož změnou můžeme změnit velikost a druh nelinearity. Hranicí, kdy se mění druh nelinearity, je hodnota nula. Je-li
je parametr, jehož změnou můžeme změnit velikost a druh nelinearity. Hranicí, kdy se mění druh nelinearity, je hodnota nula. Je-li  nulová, potom závislost momentu v pružině na výchylce závěsného prutu je lineární (tuhost pružiny se nemění). Je-li
nulová, potom závislost momentu v pružině na výchylce závěsného prutu je lineární (tuhost pružiny se nemění). Je-li  větší jako nula, potom tuhost pružiny s výchylkou stoupá. Je-li menší než nula, tuhost pružiny klesá.
větší jako nula, potom tuhost pružiny s výchylkou stoupá. Je-li menší než nula, tuhost pružiny klesá.
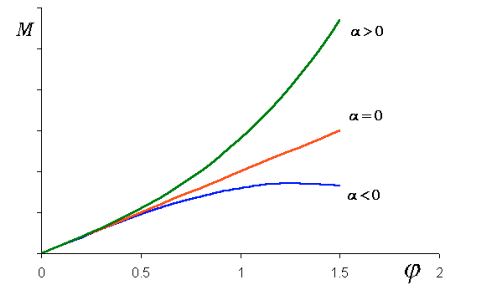 | Znázornění vlivu hodnoty  na průběh momentu M ve vetknutí v závislosti na pootočení prutu na průběh momentu M ve vetknutí v závislosti na pootočení prutu  . . |
Označení případů
Případem nazveme výpočet dynamického systému, kdy se mění pouze čas. To znamená, že počáteční podmínky a parametry se nemění. Budeme-li analyzovat závislosti na změnách počátečních podmínek či parametrů, bude se označení odvozovat od toho co mají jednotlivé případy při této změně společné. Proměnlivost dané veličiny pak bude zřejmá ze zobrazení.
Proto, abychom se nemohli splést s ohledem na množství údajů, budeme každý případ simulace jednoznačně označovat. U obrázků budou vždy uvedeny všechny parametry a počáteční podmínky, pokud nebudou proměnlivé. V analýzách závislostí se proměnlivé hodnoty proškrtnou.
Pro porovnání se objeví případ, který je geometricky lineární. Ten bude označen značkou gl. Také to znamená, že bude-li  nulová a bude-li zároveň přítomna značka gl, bude případ lineárním dynamickým systémem.
nulová a bude-li zároveň přítomna značka gl, bude případ lineárním dynamickým systémem.
Hodnoty parametrů a počátečních podmínek jsou zobrazeny bez zaokrouhlení (další desetinná místa jsou nulová), aby se výsledek v případě chaotického chování dal reprodukovat.

Omezení velikosti deformací
Dynamický systém, který jsme sestavili, připouští libovolně velké pootočení závěsného prutu. Vzhledem k naší konstrukci, kterou nahrazujeme, je to ovšem nepřípustné. Proto si pro hledání jednotlivých případů stanovíme mez extrémních deformací jako pootočení jeden plný symetrický půloblouk, tedy:

Chyba numerické metody a vytváření podivného atraktoru
Protože dynamický systém řešíme numericky, je jeho řešení pouze přibližné. Dle dynamického systému, použité numerické metody a diskretizačního kroku metody se v čase vyvíjí chyba řešení. Pochopitelným požadavkem tedy bude, aby se velikost chyby v čase příliš neměnila, a aby její vliv, vzhledem k použitému zobrazení, nebyl patrný.
Jedním úkolem bude tedy stanovení diskretizačního kroku a druhým úkolem bude vhodný způsob kontroly výsledku. Mezi těmito úkoly je zřejmá zpětná vazba. Zjistíme-li kontrolou, že chyba je příliš velká, musíme zvolit nový diskretizační krok, ovšem zároveň nechceme, aby byl krok příliš malý, protože by se zvýšila časová náročnost úlohy.
Jako kontrolu výsledku lze použít následující řešení:
Je pochopitelné, že v případě, kdy se systém chová chaoticky, bude objektivně těžké rozhodnout, zdali chyba nezpůsobí znehodnocení výsledku. I v tomto případě však lze použít naznačené kontroly. Důležitou poznámkou je potom fakt, že vlivem citlivosti systému při chaotickém chování na libovolně velké změny, bude neustále docházet k přeskakování mezi jednotlivými velmi blízkými trajektoriemi. Tento fakt způsobí, že se nevytvoří tolerovatelně přesné řešení, ale řešení pro velmi mnoho různých počátečních podmínek, které vedou k blízkým trajektoriím. Tohoto důsledku využíváme pro konstrukci podivného atraktoru, jehož zobrazení v řezu můžeme použít jako kontrolní mechanismus.
(Atraktor je vlastně celý, obsahuje totiž trajektorie pro různé počáteční podmínky, protože vlivem numerických chyb a nestability přechází řešení neustále přes blízké trajektorie.)
Pro tuto práci byla použita všechna popsaná kontrolní řešení pro funkčnost algoritmů, pro vývoj numerické chyby, i pro vytváření podivných atraktorů.
Nepřesnosti v zobrazení
Protože jako výstupní zařízení experimentu používáme počítač, dochází nutně ve všech veličinách k diskretizaci (omezení na jednotlivé body). Tato vlastnost má vliv na všechny výstupy, a proto je třeba si ji uvědomit. Z této vlastnosti také vyplývají tři problémy zobrazování. První vzniká, jestliže máme zobrazit libovolnou závislost, u které nemůžeme vyloučit nespojitost. Potom nelze takovou závislost spojovat lineární nebo libovolnou jinou interpolací. Druhým problémem je, že některou úzkou, ale výraznou oblast, nemusíme vůbec postihnout, protože prostě žádný testovaný bod do této úzké oblasti nepadl. A třetím problémem je jev, který vzniká při nízkém počtu výpočtových bodů (tzv. podvzorkování). Dochází k tomu, že vzniká nová informace, která vlastně vůbec neexistuje. Této chybě způsobené nízkou frekvencí vzorkování se říká alias. Setkáváme se s ní ve všech druzích digitalizace spojitých signálů.
 | Obrázek sbíhajících se černých čar na bílém pozadí při nedostatečném rozlišení. V obrázku vznikají ornamenty, které nemají žádný účel. Tomuto jevu se říká alias. |
Všechny experimenty, tj. všechny jednotlivé případy které si zobrazíme, jsou vypočteny s krokem h = 0.0001 s numerickou metodou klasickou Runge-Kuttovou. Je to krok, pro nějž byla chyba metody v toleranci dané zobrazením.
Experimenty jsou řazeny tak, abychom poznávali jevy a nástroje pro jejich zkoumání od nenáročných k náročnějším. Tento postup však není v souladu s postupem, jakým byl systém zkoumán.
V popisech limitních cyklů se objeví pojem energie limitního cyklu. Touto energií se myslí střední celková energie systému v ustálení (celková energie se vlivem budící síly neustále mění).
Naši prohlídku experimentů začneme tím, že si předvedeme některé výpočetní nástroje a zobrazení na lineárním systému. Přesněji to bude lineární systém takový, na který by náš zkoumaný nelineární systém zdegradoval po odstranění nelinearit. Tato degradace je možná dvěma způsoby: prvním je minimalizace dodávané energie, ať už budící silou nebo počátečními podmínkami a druhým je přímé odstranění nelinearity z dynamického systému. Vybereme druhou možnost, abychom mohli použít větších energií takových, jaké budeme používat u nelineárního systému.
Ukážeme si jediný případ geometricky i fyzikálně lineární (s geometrickou nelinearitou odstraněnou a s parametrem nelinearity  nulovým), budící frekvencí
nulovým), budící frekvencí  rovnou 10 rad.s-1 a amplitudou budící síly A rovnou 5 N. Protože je systém lineární, na její velikosti vlastně nezáleží, výsledky jsou totiž lineárně transformovatelné. Všechny ostatní parametry budou takové, jak byly předem určeny (viz část Simulace/Parametry).
rovnou 10 rad.s-1 a amplitudou budící síly A rovnou 5 N. Protože je systém lineární, na její velikosti vlastně nezáleží, výsledky jsou totiž lineárně transformovatelné. Všechny ostatní parametry budou takové, jak byly předem určeny (viz část Simulace/Parametry).
Lc0.1m0.2l0.15s3.9a5omg10
Trajektorie:
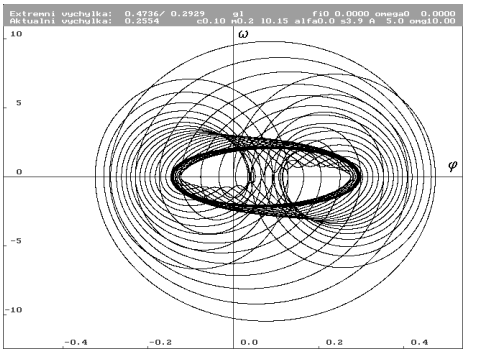 | Kompletní projekce trajektorie pro nulové počáteční podmínky. Je vidět ustalování systému do limitního cyklu. |
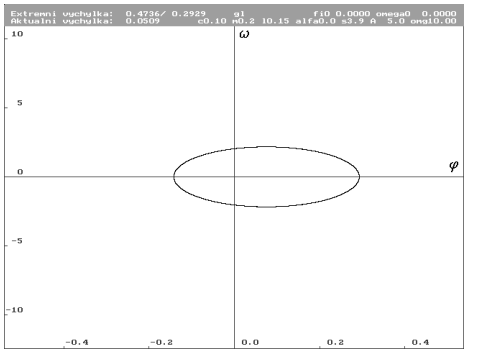 | Limitní cyklus. Zřetelně se jedná o elipsu, která je limitním cyklem každého harmonicky buzeného lineárního systému. Je umístěná excentricky, což je způsobeno působením gravitační síly. |
Řezy - Poincarého mapy:
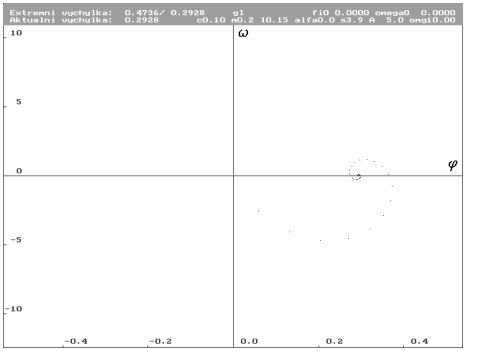 | Kompletní řez (Poincarého mapa) trajektorie. Body leží na spirále se středem v bodu, který je bodem v řezu limitním cyklem. |
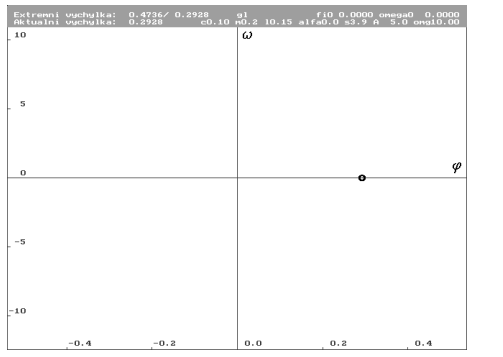 | Poincarého mapa limitního cyklu se zvýrazněním. Bod leží velmi blízko osy úhlové výchylky
 . Jeho blízkost k této ose je dána velikostí tlumení (čím větší je útlum, tedy parametr útlumu c, tím dále je bod od osy . Jeho blízkost k této ose je dána velikostí tlumení (čím větší je útlum, tedy parametr útlumu c, tím dále je bod od osy  ). ). |
Závěrem:
Ukázali jsme si, že limitním cyklem harmonicky buzeného lineárního systému je elipsa, která je v Poincarého mapě bodem. To mimochodem dokládá vhodnost způsobu provádění řezu. Jakékoliv zmnožení bodů v řezu limitního cyklu bude nelineární charakteristikou systému, avšak opak neplatí (limitní cyklus nemusí být elipsou, avšak v Poincarého mapě také bude pouze bodem).
V další části si ukážeme, že přibližně lineární odezva u nelineárního systému je skutečně dosažitelná při nižších energiích a jak se mění se zvyšující se energií do nelineární.
Dynamický výpočet stavebních konstrukcí se provádí zpravidla lineární. Toto řešení zanedbává nelineární vlastnosti konstrukce a může vést k různým chybám. Někdy je důležité zjistit hranici použitelnosti těchto zjednodušených výpočtů. Lineární systém je jednoduchý v tom smyslu, že dovoluje použití analytických metod pro jeho řešení. Ale jeho zkoumáním nezjistíme právě onu hranici použitelnosti. Pro zjištění této hranice stačí do řešení zahrnout právě jen to, co tuto hranici vytváří. Bohužel tímto rozšířením můžeme ztratit analytickou řešitelnost úlohy.
Protože náš nelineární systém řešíme přímo numericky, bude snadné zjistit, při jakých parametrech se systém začne projevovat odlišně od jeho lineárního ekvivalentu. Je třeba si uvědomit, že hodnocení, kdy ekvivalentní lineární systém ztrácí reálnost, je závislé na tom, co je pro výstup z řešení podstatné. My se zaměříme na trajektorii v limitním cyklu. Víme, že limitní cyklus lineárního systému je elipsa, takže stačí srovnat tvar daného limitního cyklu s elipsou.
Ukážeme si tedy případy s nelineárním součinitelem  rovným 0.8, budící frekvencí
rovným 0.8, budící frekvencí  rovnou 10 rad.s-1 a amplitudou budící síly A proměnlivou právě tak, aby její hodnoty bylo možno považovat za přechodovou oblast. Budeme také sledovat extrémy úhlové výchylky
rovnou 10 rad.s-1 a amplitudou budící síly A proměnlivou právě tak, aby její hodnoty bylo možno považovat za přechodovou oblast. Budeme také sledovat extrémy úhlové výchylky  (klidová výchylka je 0.0749 rad). Jako doplnění si zobrazíme u okrajových případů také Poincarého mapy a vyneseme si graf ustálené extrémní výchylky v závislosti na amplitudě budící síly A.
(klidová výchylka je 0.0749 rad). Jako doplnění si zobrazíme u okrajových případů také Poincarého mapy a vyneseme si graf ustálené extrémní výchylky v závislosti na amplitudě budící síly A.
A = 0.5 N (Nc0.1m0.2l0.15alfa0.8s3.9a0.5omg10)
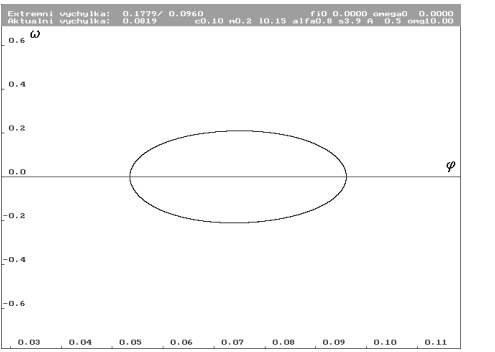 | Limitní cyklus systému s amplitudou budící síly A rovnou 0.5 N. Ustálená extrémní výchylka je přibližně desetina radiánu, což si lze představit jako decimetrovou výchylku metrového prutu. |
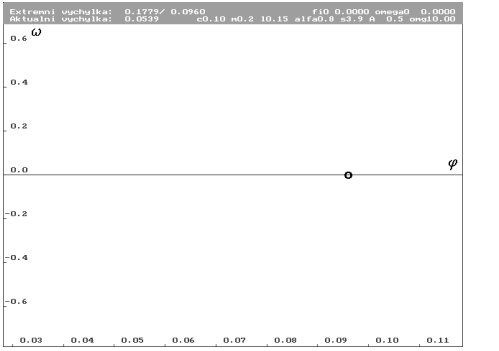 | Odpovídající Poincarého mapa se zvýrazněním. V řezu je limitní cyklus jediným bodem a leží velmi blízko osy  . . |
A = 1 N (Nc0.1m0.2l0.15alfa0.8s3.9a1omg10)
 | Limitní cyklus pro amplitudu budící síly A rovnou 1 N, tedy dvojnásobek předchozí. Ustálená extrémní výchylka se zvětšila (přírůstek je na čtyři desetinná místa přesně lineární). Na obrázku je již patrné zkřivení limitního cyklu (v tomto smyslu tedy systém již lineární není). |
A = 2 N (Nc0.1m0.2l0.15alfa0.8s3.9a2omg10)
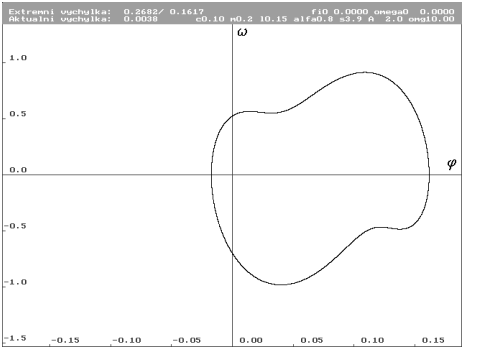 | Limitní cyklus pro A rovno 2 N. Ustálená výchylka se od lineární předpovědi liší na třetím desetinném místě a lineární předpověď, což je zvláštní, je nižší. Zkřivení je zde mnohem patrnější. Intuitivně odhaduji, že zkřivení způsobuje nárůst ustálené extrémní výchylky tím, že prodlužuje dobu, kdy je trajektorie v oblasti vyšších rychlostí. Limitní cyklus se proměňuje spojitě a hladce. |
A = 4 N (Nc0.1m0.2l0.15alfa0.8s3.9a4omg10)
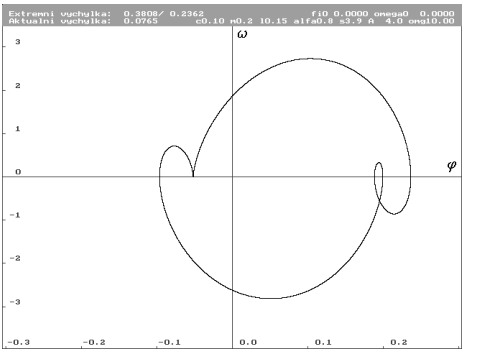 | Limitní cyklus pro A rovno 4 N. Ustálená výchylka je již výrazně odchýlena od lineární. Došlo ke výraznému snížení vypočtené ustálené extrémní výchylky oproti lineární (tedy naopak než u předchozího případu). Ze zkřivení se vytvořily smyčky, které v sobě zřejmě pohlcují část energie. |
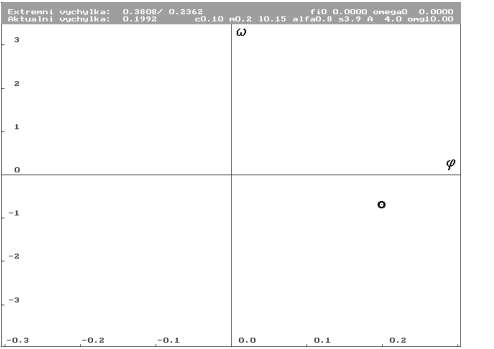 | Odpovídající Poincarého mapa se zvýrazněním. Bod je v limitním cyklu stále jen jeden, ale již je výrazně mimo osu  . . |
Závěrem:
Poznali jsme, jak probíhají změny tvaru limitních cyklů, při změnách množství energie dodávané budící silou. Poznamenejme však, že jsme viděli pouze některé stabilní změny tvaru limitních cyklů. Také je důležitou informací to, že z hlediska obecné dynamiky, jsme použili pouze malých energií, takže se limitní cyklus příliš nerozvinul.
Zobrazíme si graf ustálené extrémní výchylky. Použijeme k tomu hodnoty z jednotlivých obrázků limitních cyklů. Pro porovnání si spočítáme a vyneseme ustálený extrém výchylky lineárního ekvivalentu.
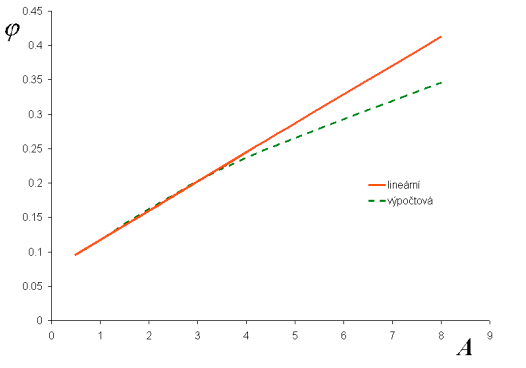 | Graf závislosti ustálené extrémní výchylky na amplitudě budící síly A. Na obrázku jsou dvě křivky. Výpočtová, která je zřetelně nelineární a druhá, která odpovídá ekvivalentní linearizaci. Výpočtová křivka se nejprve mírně nadzvedne nad lineární křivku a poté ji po snížení rychlosti vzrůstu protne. |
V dalších experimentech se podíváme podrobněji na průběh řezu limitních cyklů v závislosti na změně amplitudy budící síly a ukážeme si jiné změny tvaru limitních cyklů.
V předchozí části jsme zkoumali vliv proměnlivosti jednoho parametru na tvar limitního cyklu. Nyní se o totéž pokusíme podrobněji a šířeji. Budeme postupovat opačně. Nejprve si vyneseme závislost projekce řezu limitní množiny na amplitudě budící síly A a potom budeme zkoumat jednotlivé zajímavé oblasti.
Tato experimentální část bude zároveň sloužit jako rozbor konstrukce bifurkačního diagramu, který je pro zkoumání systému velmi důležitý. Bifurkační diagramy nás totiž budou provázet i dalšími částmi.
Konstrukce bude probíhat následovně: pro každou hodnotu amplitudy A, tedy pro každý případ, provedeme skrytou simulaci trvající určitou, předem stanovenou dobu. Po uplynutí této doby (tohoto množství iterací) předpokládáme, že systém se dostatečně přiblížil k limitní množině. Dále simulaci necháme pokračovat a provedeme zvolený počet řezů touto limitní množinou (např. padesát) a tyto řezy promítneme do osy  . Tento promítnutý řez zobrazíme na plochu s osami proměnlivého parametru A a úhlové výchylky
. Tento promítnutý řez zobrazíme na plochu s osami proměnlivého parametru A a úhlové výchylky  . Výsledkem tedy bude řada projekcí řezů.
. Výsledkem tedy bude řada projekcí řezů.
Neproměnlivé parametry případů budou stejné jako v předchozí části, tj. nelineární součinitel  rovný 0.8, budící frekvence
rovný 0.8, budící frekvence  rovná 10 rad.s-1. Amplituda budící síly A bude tentokrát přibližně takového rozsahu, abychom nepřekročili stanovenou mez extrémních deformací.
rovná 10 rad.s-1. Amplituda budící síly A bude tentokrát přibližně takového rozsahu, abychom nepřekročili stanovenou mez extrémních deformací.
Biffi a0 64 (Nc0.1m0.2l0.15alfa0.8s3.9omg10)
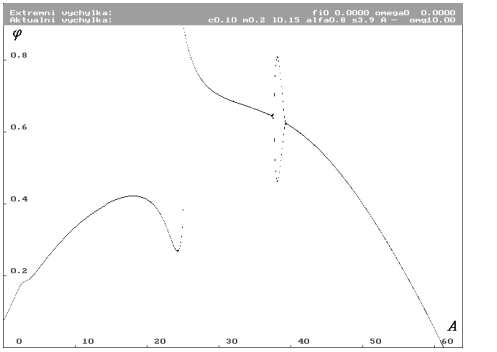 | Bifurkační diagram pro parametr amplituda budící síly A v rozsahu 0 až 64 N se 640 vzorky (jednotlivými případy; řezy) v ekvidistantní síti. Lze dobře rozeznat počáteční lineární průběh. Také jsou vidět dvě zvláštní oblasti. První oblastí je náhlá změna polohy bodu v řezu a druhou oblastí je rozdvojení (bifurkace) bodu v řezu. |
Limitní cykly z oblasti náhlého přechodu:
A = 20 N (Nc0.1m0.2l0.15alfa0.8s3.9a20omg10)
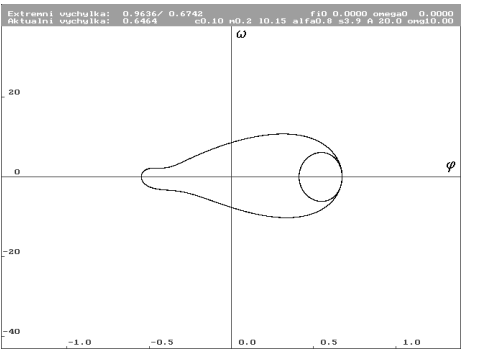 | Limitní cyklus pro A rovno 20 N. Limitní cyklus s rozvinutou smyčkou a s rozvíje-jícím se zkřivením v levé části limitního cyklu. |
A = 22 N (Nc0.1m0.2l0.15alfa0.8s3.9a22omg10)
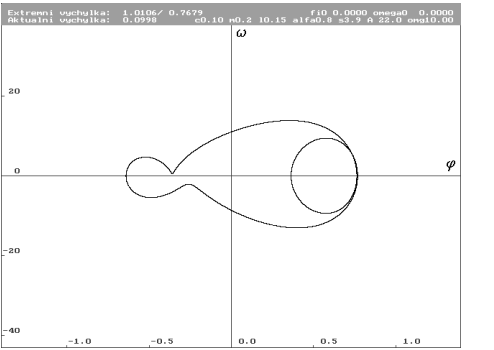 | Limitní cyklus pro A rovno 22 N. Ze zkřivení se začínají vytvářet nové smyčky. |
A = 24.2 N (Nc0.1m0.2l0.15alfa0.8s3.9a24.2omg10)
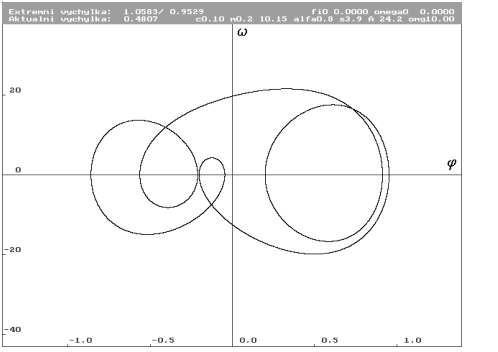 | Limitní cyklus pro A rovno 24.2 N. Obě nové smyčky se rozvinuly, stará smyčka se destabilizuje. Celkově má limitní cyklus podstatně vyšší energii. Stav z lokálního minima na bifurkačním diagramu, těsně před náhlou změnou. Systém jakoby se snažil pohltit přibývající energii vyvářením nových smyček, ale ty už k pohlcení nestačí. |
A = 25 N (Nc0.1m0.2l0.15alfa0.8s3.9a25omg10)
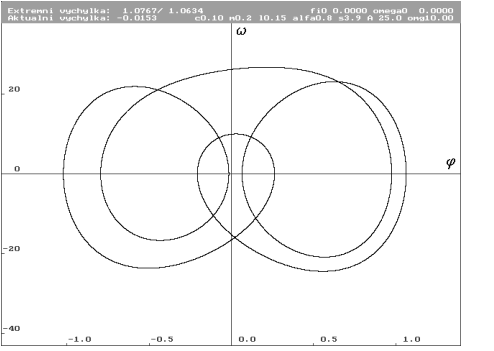 | Limitní cyklus pro A rovno 25 N. Další rychlé zvýšení energie. Stav při náhlé změně (nacházíme se na hrotu vzestupné větve množiny bodů na bifurkačním diagramu). Změny limitního cyklu jsou spojité. |
A = 25.1 N (Nc0.1m0.2l0.15alfa0.8s3.9a25.1omg10)
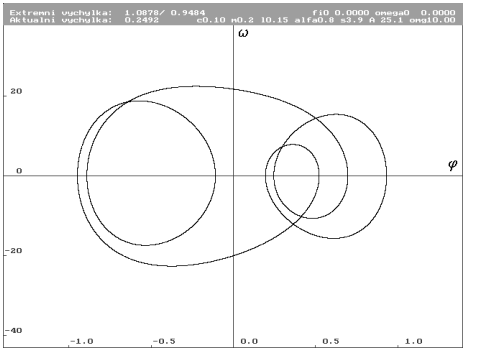 | Limitní cyklus pro A rovno 25.1 N. Stav po náhlé změně (hrot sestupné větve množiny bodů). Patrné uklidňování. Energie limitního cyklu se snižuje. V levé části se stabilizuje smyčka. Obě pravé smyčky budou zřejmě zanikat. |
A = 28 N (Nc0.1m0.2l0.15alfa0.8s3.9a28omg10)
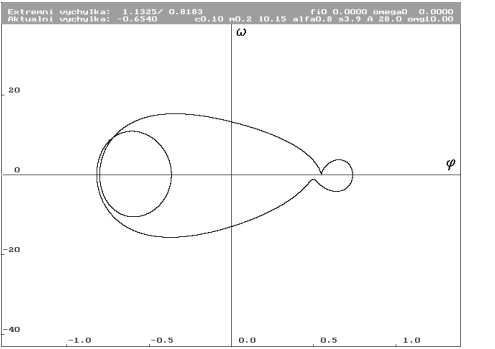 | Limitní cyklus pro A rovno 28 N. Smyčky vpravo skutečně zanikají, změny jsou již pozvolné. Pokračující uklidnění systému. |
A = 30 N (Nc0.1m0.2l0.15alfa0.8s3.9a30omg10)
 | Limitní cyklus pro A rovno 30 N. Obě pravé smyčky zanikly. |
A = 32 N (Nc0.1m0.2l0.15alfa0.8s3.9a32omg10)
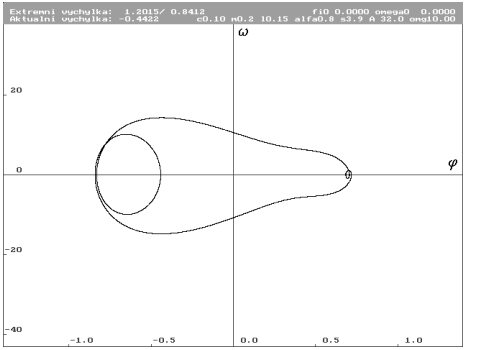 | Limitní cyklus pro A rovno 32 N. Na pravé straně se vytvořila nová smyčka poněkud odlišným způsobem. |
Limitní cykly z oblasti rozdvojení:
A = 37.5 N (Nc0.1m0.2l0.15alfa0.8s3.9a37.5omg10)
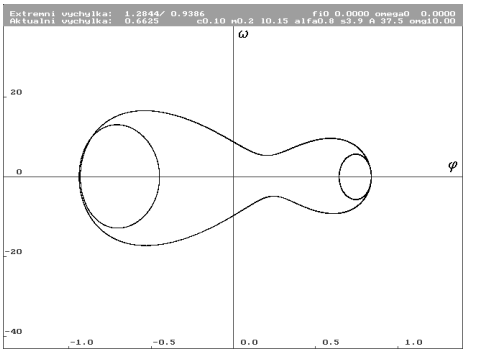 | Limitní cyklus pro A rovno 37.5 N. Dvě stabilní smyčky. Stav před rozdvojením. |
A = 37.7 N (Nc0.1m0.2l0.15alfa0.8s3.9a37.7omg10)
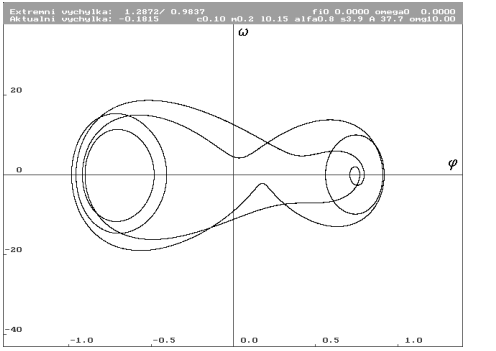 | Limitní cyklus pro A rovno 37.7 N. Stav po rozdvojení. Pokus upřesnit místo rozdvo-jení selhává na časové náročnosti. |
A = 38 N (Nc0.1m0.2l0.15alfa0.8s3.9a38omg10)
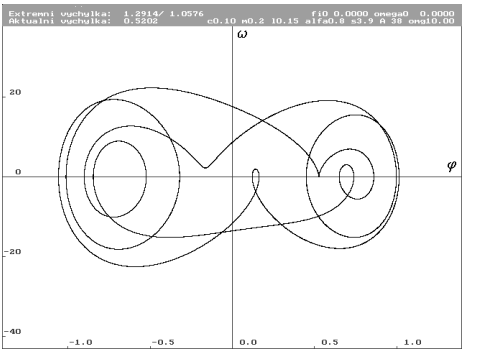 | Limitní cyklus pro A rovno 38 N. Téměř vrchol rozdvojení. Vzrostla energie limit-ního cyklu. |
A = 39 N (Nc0.1m0.2l0.15alfa0.8s3.9a39omg10)
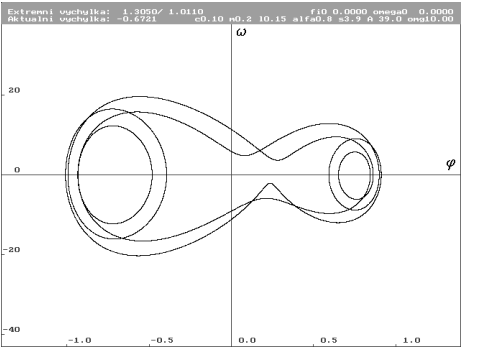 | Limitní cyklus pro A rovno 39 N. Systém se uklidňuje. |
A = 39.2 N (Nc0.1m0.2l0.15alfa0.8s3.9a39,2omg10)
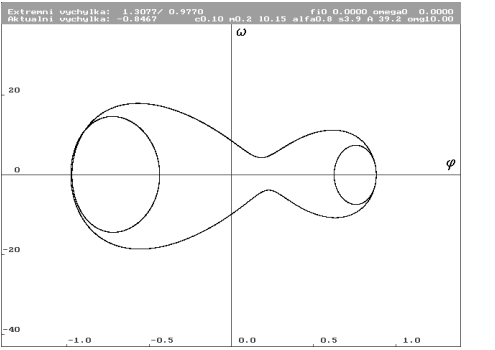 | Limitní cyklus pro A rovno 39.2 N. Těsně po spojení. Cyklus je podobný cyklu před rozdvojením, ale má trochu více energie. |
Limitní cyklus ze závěru diagramu:
A = 60 N (Nc0.1m0.2l0.15alfa0.8s3.9a60omg10)
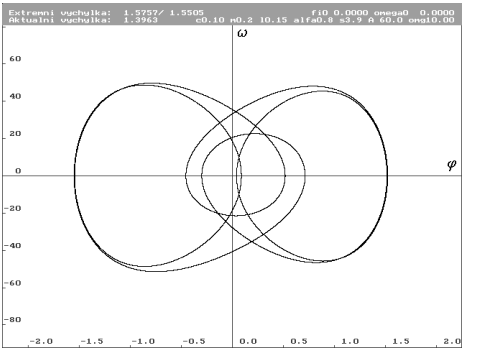 | Limitní cyklus pro A rovno 60 N. Extrémní výchylka je již příliš veliká. Z obrázku je vidět, že systém ze zkřivení ve středních částech předchozího obrázku vytvořil smyčky. Obě okrajové smyčky jsou stále stabilní. Je třeba si uvědomit, že tento obrázek má jiné, hrubější dělení os. Předchozí obrázky měly dělení os vzájem-ně stejné. |
Závěrem:
Byli jsme svědky dvou velmi rychlých proměn limitního cyklu. Je zřejmé, že místa těchto proměn jsou význačnými hodnotami parametru budící síly A. Každá z proměn se však navzdory očekávání dramatičtějšího průběhu později ustálila.
V dalších experimentech budeme sledovat, co se stane zvýšíme-li nelinearitu systému pomocí nelineárního součinitele  .
.
Přesvědčili jsme se, že nelinearita obohacuje chování systému novými neobvyklými jevy, které lineární systémy vůbec neznají. Protože jsme u systému s nelineárním součinitelem  rovným 0.8 vyčerpali extrémní možnou výchylku, pokusíme se tento součinitel zvýšit a znovu provést analýzu pomocí bifurkačního diagramu.
rovným 0.8 vyčerpali extrémní možnou výchylku, pokusíme se tento součinitel zvýšit a znovu provést analýzu pomocí bifurkačního diagramu.
Zvýšení součinitele  způsobí, že se zvýší rychlost vzrůstu tuhosti pružiny, takže pro dosažení meze extrémních deformací bude zapotřebí více energie dodávané budící silou.
způsobí, že se zvýší rychlost vzrůstu tuhosti pružiny, takže pro dosažení meze extrémních deformací bude zapotřebí více energie dodávané budící silou.
Budeme studovat případy s nelineárním součinitelem  násobeným šesti (tedy 4.8), budící frekvencí
násobeným šesti (tedy 4.8), budící frekvencí  rovnou 10 rad.s-1 a amplituda budící síly A bude opět proměnlivá.
rovnou 10 rad.s-1 a amplituda budící síly A bude opět proměnlivá.
Biffi a0 192 (Nc0.1m0.2l0.15alfa4.8s3.9omg10)
 | Bifurkační diagram pro parametr A proměnlivý od 0 do 192 N, s 1920 vzorky v ekvidistantní síti. Na obrázku jsou patrné oblasti chaotického chování. Iterační mez pro vykreslení bifurkačního diagramu nabyla příliš vysoká, proto jsou v některých částech diagramu nepodstatné nepřesnosti. Podíváme se podrobněji na trajektorie ze dvou oblastí chaotického chování s nižší energií. Vybereme případy s A = 120 N a A = 145 N. |
Trajektorie a její řezy z oblasti chaotického chování:
A = 120 N (Nc0.1m0.2l0.15alfa4.8s3.9a120omg10)
 | Trajektorie pro A rovno 120 N. Je vidět, že se systém vyvíjí chaoticky. Projekce trajektorie již zřetelně nestačí pro dobré zobrazení vývoje. |
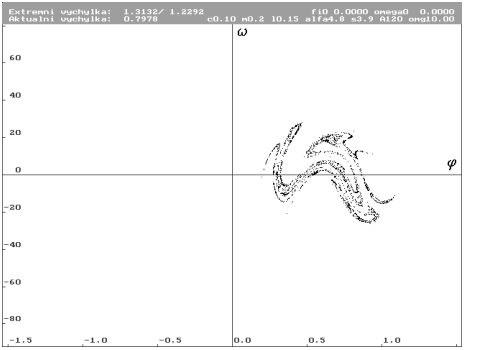 | Odpovídající Poincarého mapa stejného měřítka. Zobrazení je již mnohem vhodnější. Útvar je zřetelně fraktál. Provedeme si jeho zvětšení. |
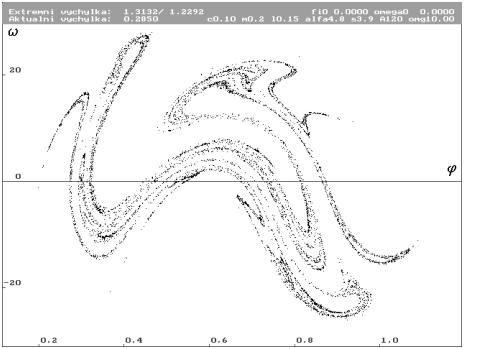 | Odpovídající Poincarého mapa. Zvětšení útvaru. Z obrázku je mnohem lépe patrná struktura. |
A = 145 N (Nc0.1m0.2l0.15alfa4.8s3.9a145omg10)
 | Trajektorie pro A rovno 145 N. Stejné měřítko jako v předchozím případě. Patrné zvýšení energie. |
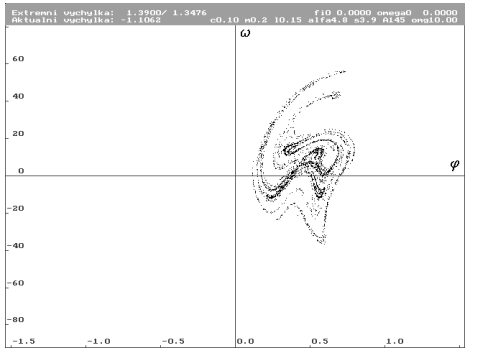 | Odpovídající Poincarého mapa ve stejném měřítku. |
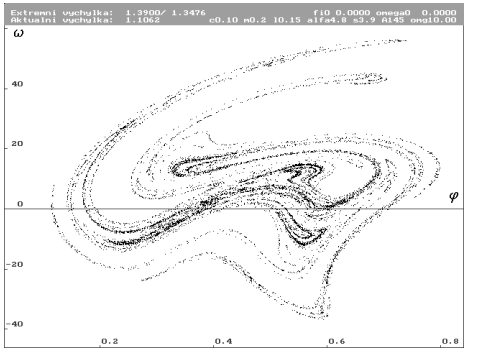 | Odpovídající Poincarého mapa. Zvětšení útvaru. |
Závěrem:
Systém se při zvýšení nelinearity začal pro některé hodnoty parametru A chovat chaoticky. Kdybychom prováděli záznam takového chování v praktické zkoušce, bez znalostí, které jsme získali, považovali bychom pravděpodobně takový záznam za znehodnocený, či zatížený nějakou vlivnou nejistotou. Avšak to by byl chybný závěr. Systém si toto chování svou nestabilitou sám vytváří.
Důležité je, že i přes nepredikovatelný pohyb systému v chaotickém režimu, v něm existuje jistý řád, který nám zaručuje uzavřenost atraktoru a tím i jeho možný posudek.
Funkce extrému stavové proměnné
V části Přechod lineárního chování jsme si poprvé vynesli graf závislosti extrému stavové proměnné (ustálené úhlové výchylky) na nějakém parametru (amplitudě budící síly). Nyní si provedeme totéž podrobněji. Vykreslíme si funkce extrému úhlové výchylky j jak ustálené, tak absolutní. Absolutní extrémní výchylka nám řekne, jaké největší výchylky bylo při celé simulaci dosaženo. Tento absolutní extrém dává hodnotu výchylky určující napjatost pro posouzení konstrukce. My budeme vyšetřovat závislost těchto dvou extrémů na obou parametrech budící síly.
V části Nástroje/Zobrazení/Funkce stavové proměnné jsme si zobrazili funkci frekvenční odezvy lineárního oscilátoru. Na tomto obrázku je vidět vztah ustálené a absolutní extrémní výchylky. Totiž, když je v tomto případě systém v rezonanci, dochází k tomu, že splývá ustálená a absolutní extrémní výchylka. Je to dáno tím, že se trajektorie v rezonanci lineárního systému přibližuje k limitnímu cyklu zevnitř, pokud to počáteční podmínky dovolí.
Je třeba si uvědomit, že absolutní extrémní výchylka je přímo závislá na počátečních podmínkách, kdežto ustálená extrémní výchylka na počátečních podmínkách přímo nezávisí. U nelineárních systémů může ustálená extrémní výchylka nepřímo záviset na počátečních podmínkách pouze v případě, že existuje více limitních cyklů, což je u našeho systému možné. Touto závislostí se ale budeme zabývat později (viz další část Bazény přitažlivosti).
Jako základní, nám bude sloužit případ s nelineárním součinitelem  rovným 0.8, budící frekvencí
rovným 0.8, budící frekvencí  rovnou 10 rad.s-1 a amplitudou budící síly A rovnou 1 N. Oba parametry budící síly však budeme střídavě měnit a prohlédneme si také rezonanční trajektorie.
rovnou 10 rad.s-1 a amplitudou budící síly A rovnou 1 N. Oba parametry budící síly však budeme střídavě měnit a prohlédneme si také rezonanční trajektorie.
 = 10 s-1 (Fexfi a0 64 (Nc0.1m0.2l0.15alfa0.8s3.9omg10))
= 10 s-1 (Fexfi a0 64 (Nc0.1m0.2l0.15alfa0.8s3.9omg10))
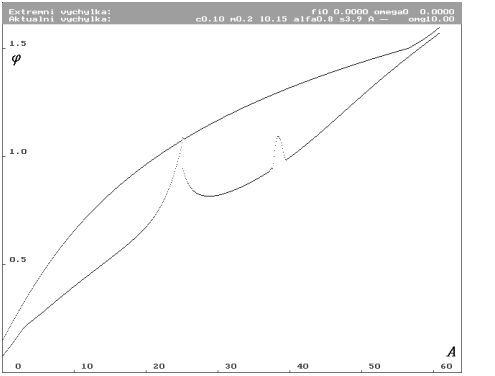 | Funkce extrému úhlové výchylky  pro budící frekvenci pro budící frekvenci  rovnou 10 rad.s-1. Amplituda budící síly A je proměnlivá od 0 N do 64 N se 640 vzorky. Na obrázku jsou dvě množiny bodů. Horní je absolutní extrémní výchylka a dolní ustálená extrémní výchylka. Obrázek navazuje na bifurkační diagram ze stejnojmenné části. Jsou zde patrny obě oblasti náhlého zvýšení energie limitního cyklu (tedy vlastně rezonance), které se kryjí s analyzovanými oblastmi z bifurkačního diagramu. rovnou 10 rad.s-1. Amplituda budící síly A je proměnlivá od 0 N do 64 N se 640 vzorky. Na obrázku jsou dvě množiny bodů. Horní je absolutní extrémní výchylka a dolní ustálená extrémní výchylka. Obrázek navazuje na bifurkační diagram ze stejnojmenné části. Jsou zde patrny obě oblasti náhlého zvýšení energie limitního cyklu (tedy vlastně rezonance), které se kryjí s analyzovanými oblastmi z bifurkačního diagramu. |
A = 1 N (Fexfi omg0 64 (Nc0.1m0.2l0.15alfa0.8s3.9a1))
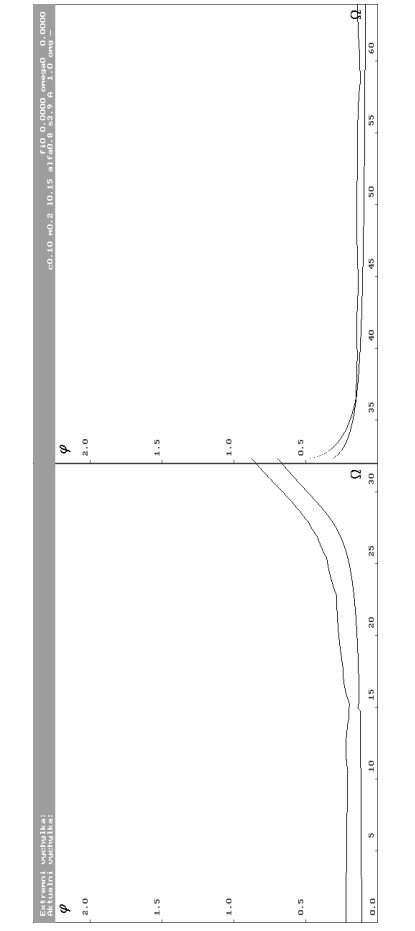 | Funkce extrému výchylky pro amplitudu budící síly A rovnu 1 N. Frekvence budící síly  proměnlivá od 0 rad.s-1 do 64 rad.s-1 s 1280 vzorky. Na obrázku je vidět oblast rezonance. Hlavní rezonanční frekvence je 32.33 rad.s-1. V pravé části uprostřed je taktéž patrná malá rezonance s frekvencí 14.95 rad.s-1. proměnlivá od 0 rad.s-1 do 64 rad.s-1 s 1280 vzorky. Na obrázku je vidět oblast rezonance. Hlavní rezonanční frekvence je 32.33 rad.s-1. V pravé části uprostřed je taktéž patrná malá rezonance s frekvencí 14.95 rad.s-1. |
Limitní cykly a trajektorie z oblastí rezonance systému A = 1 N:
 = 32.33 rad.s-1
= 32.33 rad.s-1 = 32.33 rad.s-1 (Nc0.1m0.2l0.15alfa0.8s3.9a1omg32.33)
= 32.33 rad.s-1 (Nc0.1m0.2l0.15alfa0.8s3.9a1omg32.33)
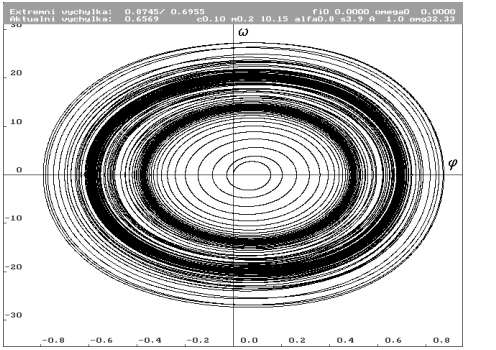 | Kompletní projekce trajektorie pro nulové počáteční podmínky. Parametr frekvence budící síly  roven 32.33 rad.s-1 (vrchol rezonance pro tyto počáteční podmínky). Ve vnějším zhuštění trajektorie je limitní cyklus. Vnitřní zhuštění trajektorie naznačuje jinou hranici extrémní energie (pravděpodobně existuje či vzniká jiný limitní cyklus). roven 32.33 rad.s-1 (vrchol rezonance pro tyto počáteční podmínky). Ve vnějším zhuštění trajektorie je limitní cyklus. Vnitřní zhuštění trajektorie naznačuje jinou hranici extrémní energie (pravděpodobně existuje či vzniká jiný limitní cyklus). |
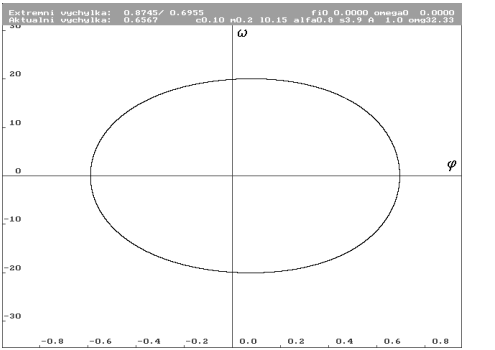 | Odpovídající limitní cyklus. Stejné měřítko. Je vidět, že limitní cyklus netvoří obálku trajektorie. To způsobuje, že se v rezonanci bodová pole ustálené a abso-lutní extrémní výchylky k sobě nepřib-ližují. |
 = 32.34 rad.s-1 (Nc0.1m0.2l0.15alfa0.8s3.9a1omg32.34)
= 32.34 rad.s-1 (Nc0.1m0.2l0.15alfa0.8s3.9a1omg32.34)
 | Kompletní projekce trajektorie pro nulové počáteční podmínky. Parametr frekvence budící síly  roven 32.34 rad.s-1 (těsně za vrcholem rezonance pro tyto počáteční podmínky). Náhlý přechod na nový limitní cyklus. Vnější zhuštění je předpovězenou hranicí extrémní energie. Nový limitní cyklus opět ve vnitřním zhuštění. roven 32.34 rad.s-1 (těsně za vrcholem rezonance pro tyto počáteční podmínky). Náhlý přechod na nový limitní cyklus. Vnější zhuštění je předpovězenou hranicí extrémní energie. Nový limitní cyklus opět ve vnitřním zhuštění. |
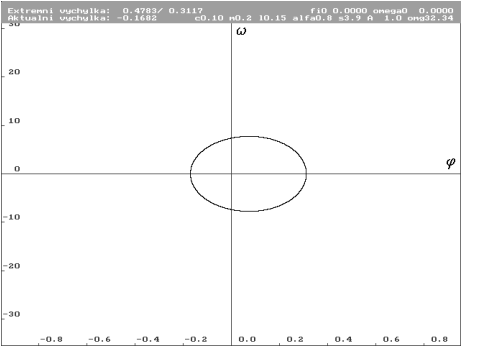 | Odpovídající limitní cyklus. Stále stejné měřítko. Vypadá to, že pro tento systém jsou v hlavní rezonanci limitní cykly velmi podobné elipse. |
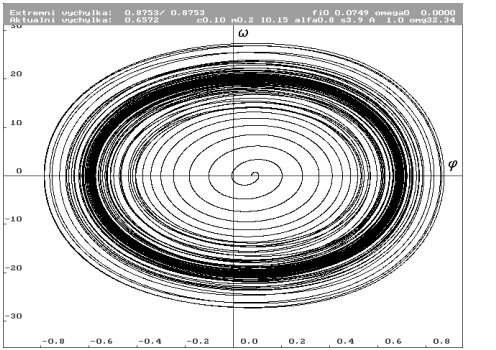 | Kompletní projekce trajektorie pro počáteční podmínky klidového stavu s působící gravitační silou (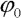 = 0.0749 rad). Parametr frekvence budící síly = 0.0749 rad). Parametr frekvence budící síly  je stále roven 32.34 rad.s-1. Je vidět, že pro tyto počáteční podmínky zatím nebylo rezonančního vrcholu dosaženo (podrob-nou hysterezní analýzou byl zjištěn vrchol na je stále roven 32.34 rad.s-1. Je vidět, že pro tyto počáteční podmínky zatím nebylo rezonančního vrcholu dosaženo (podrob-nou hysterezní analýzou byl zjištěn vrchol na  rovno 41.78 rad.s-1). Potvrzena současná existence více limitních cyklů. Ani pro tyto počáteční podmínky nebyl absolutní extrém výchylky na limitním cyklu. rovno 41.78 rad.s-1). Potvrzena současná existence více limitních cyklů. Ani pro tyto počáteční podmínky nebyl absolutní extrém výchylky na limitním cyklu. |
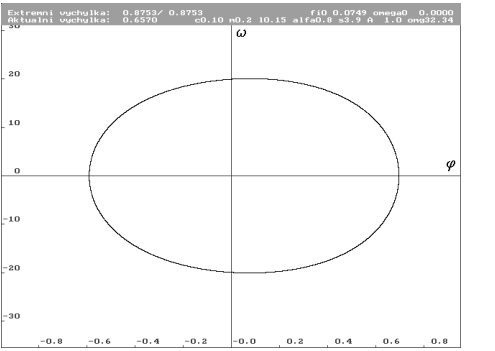 | Odpovídající limitní cyklus. |
 = 14.95 rad.s-1
= 14.95 rad.s-1 = 14.9 rad.s-1 (Nc0.1m0.2l0.15alfa0.8s3.9a1omg14.9)
= 14.9 rad.s-1 (Nc0.1m0.2l0.15alfa0.8s3.9a1omg14.9)
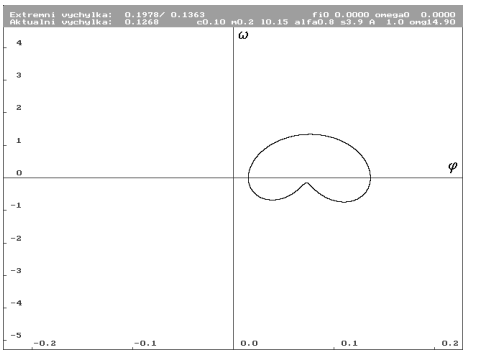 | Limitní cyklus před rezonančním vrcholem pro budící frekvenci  rovnou 14.9 rad.s-1. rovnou 14.9 rad.s-1. |
 = 14.95 rad.s-1 (Nc0.1m0.2l0.15alfa0.8s3.9a1omg14.95)
= 14.95 rad.s-1 (Nc0.1m0.2l0.15alfa0.8s3.9a1omg14.95)
 | Limitní cyklus ve vrcholu dílčí rezonance pro  rovno 14.95 rad.s-1. rovno 14.95 rad.s-1. |
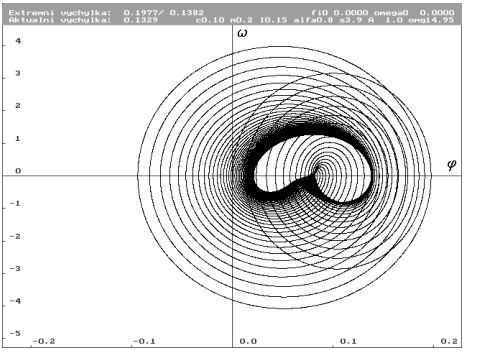 | Odpovídající kompletní trajektorie pro nulové počáteční podmínky. Je vidět, že ani pro tuto rezonanci počáteční podmínky nedovolily vytvořit absolutní extrémní výchylku na limitním cyklu. |
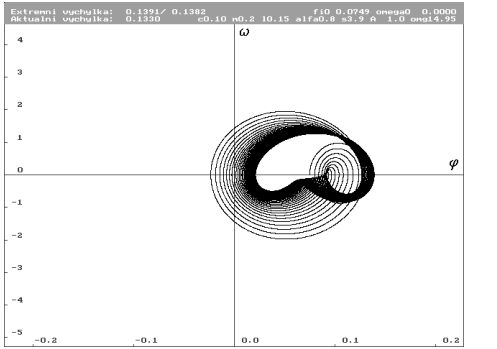 | Trajektorie pro počáteční podmínky klidového stavu s působící gravitační silou. Snížení vlivu počátečních podmínek na absolutní extrémní výchylku. Stále je ovšem ustálená extrémní výchylka menší. |
 = 15 rad.s-1 (Nc0.1m0.2l0.15alfa0.8s3.9a1omg15)
= 15 rad.s-1 (Nc0.1m0.2l0.15alfa0.8s3.9a1omg15)
 | Limitní cyklus za rezonančním vrcholem pro budící frekvenci  rovnou 15 rad.s-1. rovnou 15 rad.s-1. |
Vypadá to, že vedlejší rezonance probíhá klidněji. Nevznikl nový limitní cyklus. Extrémní ustálená výchylka vytváří vrchol spojitě, k čemuž u hlavní rezonance nedošlo.
Nyní si zvýšíme energii dodávanou budící silou a znovu si vykreslíme funkci extrému výchylky. Parametr amplituda budící síly A zvýšíme patnáctkrát, bude tedy roven 15 N.
A = 15 N (Fexfi omg0 64 (Nc0.1m0.2l0.15alfa0.8s3.9a15))
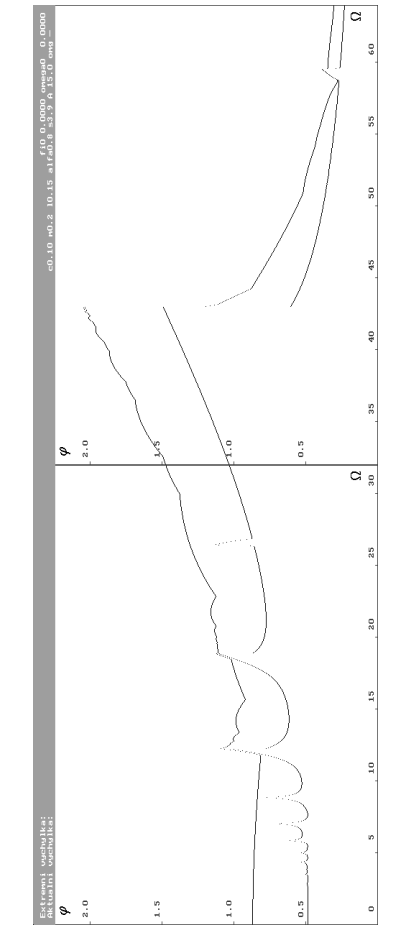 | Funkce extrému výchylky pro amplitudu budící síly A rovnu 15 N. Frekvence budící síly  proměnlivá v od 0 rad.s-1 do 64 rad.s-1 s 1280 vzorky. Na obrázku je vidět více výrazných oblastí rezonance. Hlavní rezonanční frekvence je 42.96 rad.s-1. Vedlejší rezonance již vytvářejí skoky. proměnlivá v od 0 rad.s-1 do 64 rad.s-1 s 1280 vzorky. Na obrázku je vidět více výrazných oblastí rezonance. Hlavní rezonanční frekvence je 42.96 rad.s-1. Vedlejší rezonance již vytvářejí skoky. |
Závěrem:
Poznali jsme, že funkce extrému stavové proměnné vhodně doplňuje bifurkační diagram. Vyjadřuje výrazné nelineární jevy specifičtějším způsobem. Z toho co jsme viděli se dá říct, že výrazný jev se projeví rychlým nárůstem energie limitního cyklu a tím se zvýší i extrémní výchylka. Pro výsledný praktický posudek konstrukce je to výborný nástroj.
Zkoumali jsme i vliv počátečních podmínek na vztah mezi absolutní a ustálenou extrémní výchylkou. Bez dalších analýz však nejsme schopni říci, zdali je při rezonanci rozdíl obou funkcí způsoben počátečními podmínkami, nebo jsou při rezonanci počáteční podmínky vedoucí k dosažení absolutního extrému výchylky v ustálení nepravděpodobné.
Zjistili jsme, že se v hlavní rezonanci vyskytují dva limitní cykly. Zkoumání rozsahu jejich současné existence je však mimo časovou dostupnost této práce. Podstatné je, že hlavní rezonance probíhá úplně jinak než u lineárního systému a to i při relativně malé energii a malých výchylkách.
Existence více limitních cyklů se projevuje v zobrazeních jako náhlý skok. Tyto skoky jsme viděli již dříve v bifurkačních diagramech. V další části se tedy na ně podrobněji zaměříme.
Při zkoumání bifurkačních diagramů i funkcí extrému výchylky jsme objevili důležitou vlastnost nelineárního systému. Touto vlastností je náhlá změna limitního cyklu při malé změně vybraného parametru. V obou zobrazeních se tato změna ukáže jako náhlá změna funkční hodnoty. Tato změna je důsledkem faktu, že se překročila hranice nutná pro přechod mezi limitním cyklem jedním a limitním cyklem druhým. O tom, který limitní cyklus zvítězí při pokusu o záchyt systému, rozhodují počáteční podmínky, které mu udělují různou trajektorii. Protože jsme všechny bifurkační diagramy i funkce extrému výchylky konstruovali s počátečními podmínkami pro každý případ stejnými, zobrazily se vždy jen body příslušné k jednomu limitnímu cyklu. Každý z limitních cyklů však může mít v přechodové části množinu počátečních podmínek, které tvoří oblast záchytu daného limitního cyklu. Tyto množiny a jejich rozložení budeme nyní sledovat.
Kriteriem pro rozpoznání limitního cyklu bude jeho úhlová výchylka v řezu limitní množiny. Po určení limitního cyklu se potom dané počáteční podmínky vhodně označí.
Pro hledání bazénů přitažlivosti, si zvolíme systém s parametry stejnými jako při konstrukci bifurkačního diagramu v části Chaotické chování. Tedy nelineární součinitel  rovný 4.8, budící frekvenci
rovný 4.8, budící frekvenci  rovnou 10 rad.s-1 a amplitudu A volenou z vybraných míst náhlých přechodů.
rovnou 10 rad.s-1 a amplitudu A volenou z vybraných míst náhlých přechodů.
Počáteční podmínky budeme volit tak, abychom pokryli co možná největší plochu z roviny počátečních podmínek, tedy počáteční úhlovou výchylku 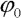 od -1.5 rad do 1.5 rad a počáteční úhlovou rychlost
od -1.5 rad do 1.5 rad a počáteční úhlovou rychlost 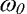 od -50 rad.s-1 do 50 rad.s-1. Rozsah této plochy sice bude přesahovat mez danou extrémní výchylkou, ale to nebude na závadu pro lepší vhled do tvaru bazénů.
od -50 rad.s-1 do 50 rad.s-1. Rozsah této plochy sice bude přesahovat mez danou extrémní výchylkou, ale to nebude na závadu pro lepší vhled do tvaru bazénů.
A = 11.5 N (Nc0.1m0.2l0.15alfa4.8s3.9a11.5omg10)
 | Limitní cyklus pro počáteční podmínky nulové. Úhlová výchylka  má v řezu hodnotu 0.0954 rad. Limitní cyklus bude v bazénu přitažlivosti zobrazen šedou barvou. má v řezu hodnotu 0.0954 rad. Limitní cyklus bude v bazénu přitažlivosti zobrazen šedou barvou. |
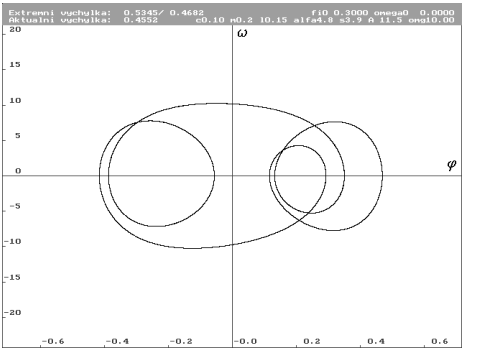 | Limitní cyklus pro počáteční podmínky 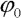 = 0.3 rad a = 0.3 rad a 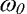 nulová. Úhlová výchylka nulová. Úhlová výchylka  má v řezu hodnotu 0.4552 rad. Limitní cyklus bude zobrazen v bayénu bílou barvou. má v řezu hodnotu 0.4552 rad. Limitní cyklus bude zobrazen v bayénu bílou barvou. |
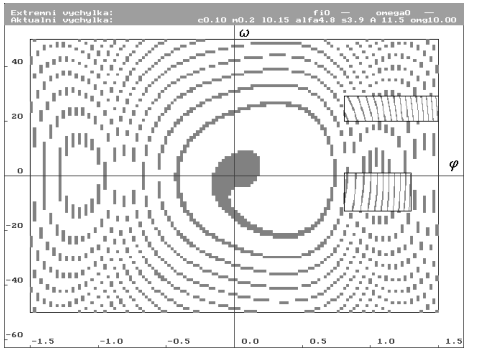 | Bazény přitažlivosti pro amplitudu budící síly A rovnou 11.5 N. Dva nalezené limitní cykly. Základní vzorkování 128 krát 96 vzorků ekvidistantně. V pravé a levé části se vyskytuje alias. Odhalen pomocí dvou oblastí zpřesnění. Bazény vytvářejí spirálu s hladkými hranicemi. |
A = 72.8 N (Nc0.1m0.2l0.15alfa4.8s3.9a72.8omg10)
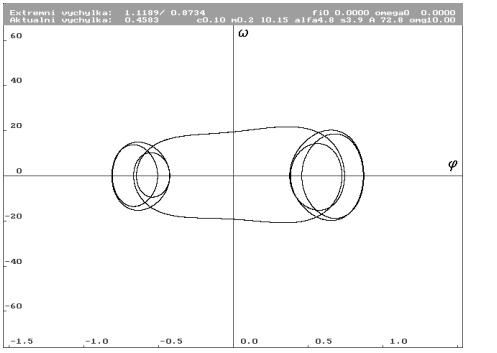 | Limitní cyklus pro počáteční podmínky nulové. Úhlová výchylka  má v řezu hodnotu 0.4583 rad. Limitní cyklus bude zobrazen šedou barvou. má v řezu hodnotu 0.4583 rad. Limitní cyklus bude zobrazen šedou barvou. |
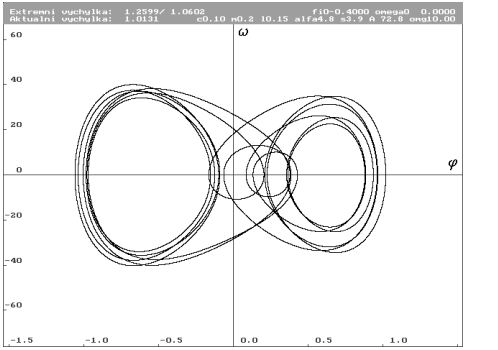 | Limitní cyklus pro počáteční podmínky 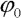 = -0.4 rad a = -0.4 rad a 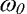 nulová. Úhlová výchylka nulová. Úhlová výchylka  má v řezu dvojí hodnotu 0.9357 rad a 1.0131 rad. Limitní cyklus bude zobrazen bílou barvou. má v řezu dvojí hodnotu 0.9357 rad a 1.0131 rad. Limitní cyklus bude zobrazen bílou barvou. |
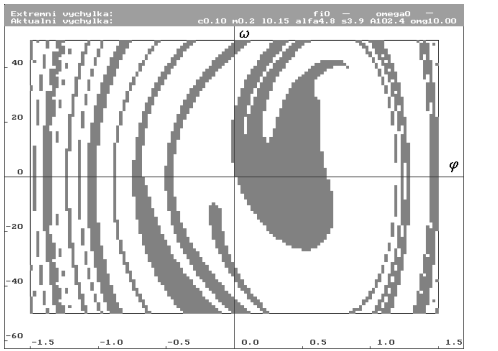 | Bazény přitažlivosti pro amplitudu budící síly A rovnou 72.8 N. Dva nalezené limitní cykly. Základní vzorkování 128 krát 96 vzorků ekvidistantně. Bazény vytvářejí již členitější hranici, avšak stále hladkou. |
A = 102.4 N (Nc0.1m0.2l0.15alfa4.8s3.9a102.4omg10)
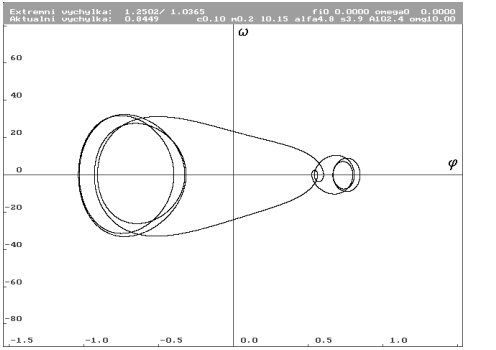 | Limitní cyklus pro počáteční podmínky nulové. Úhlová výchylka  má v řezu hodnotu 0.8449 rad. Limitní cyklus bude v bazénu zobrazen světle šedou barvou. má v řezu hodnotu 0.8449 rad. Limitní cyklus bude v bazénu zobrazen světle šedou barvou. |
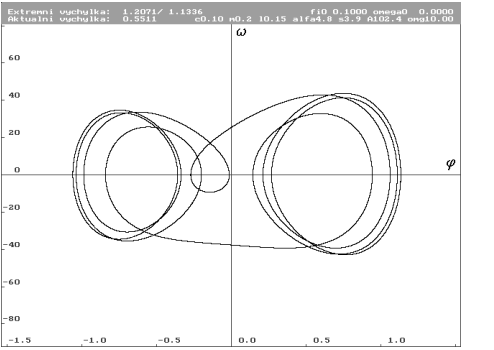 | Limitní cyklus pro počáteční podmínky 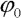 = 0.1 rad a = 0.1 rad a 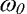 nulová. Úhlová výchylka nulová. Úhlová výchylka  má v řezu hodnotu 0.5511 rad, ale při řešení kolísá. Limitní cyklus bude zobrazen tmavě šedou barvou. má v řezu hodnotu 0.5511 rad, ale při řešení kolísá. Limitní cyklus bude zobrazen tmavě šedou barvou. |
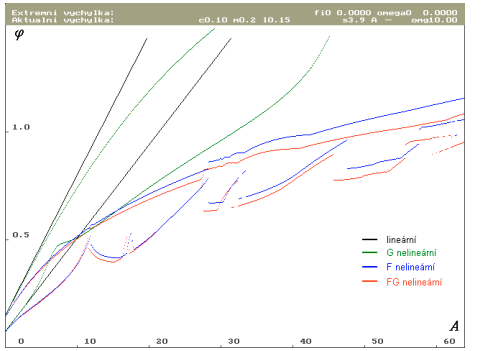
 | Neustálená trajektorie pro počáteční podmínky 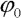 = 0.05 rad a = 0.05 rad a 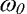 nulová. Úhlová výchylka nulová. Úhlová výchylka  je proměnlivá v poměrně velkém rozsahu. Zřejmě chaotický vývoj. Trajektorie bude zobrazena bílou barvou. je proměnlivá v poměrně velkém rozsahu. Zřejmě chaotický vývoj. Trajektorie bude zobrazena bílou barvou. |
 | Bazény přitažlivosti pro amplitudu budící síly A rovnou 102.4 N. Dva nalezené limitní cykly a třetí neustálený. Základní vzorkování 128 krát 96 vzorků ekvidistantně. Bazény jsou ohraničeny zřejmě fraktální hranicí. Bazén tmavě šedého limitního cyklu je neuspořádaný. |
Závěrem:
Existence více limitních cyklů pro stejné parametry je další charakteristikou nelineárních systémů. I jejich hledání může být do jisté míry problémem. Je dokázáno, že neexistuje algoritmus, který by našel všechny limitní cykly. Někdy si tedy nemusíme být jisti, že jsme nalezli všechny limitní cykly.
Bazény přitažlivosti jsou na výpočetní čas nejnáročnějším použitým nástrojem pro studium chování systému, proto jejich rozlišení nemohlo být dostatečně jemné, avšak i tak jsme dobře rozpoznávali proměny struktury jejich hranice.
U posledního případu již rozeznávání limitních cyklů nebylo snadné a bez provedení dalších analýz nebudeme schopni rozhodnout, zdali to mělo negativní dopad na přesnost bazénů.
Jak pro kontrolu, tak pro poznání bude prospěšné, když si zobrazíme vliv jednotlivých nelineárních členů na chování systému. Protože máme dva nelineární členy, existují pouze čtyři kombinace různých systémů. Jejich vliv si zobrazíme ve společném bifurkačním diagramu a společné funkci extrému úhlové výchylky  .
.
Ve všech čtyřech systémech bude budící frekvence  rovna 10 rad.s-1, amplituda budící síly A proměnlivá od 0 N do 64 N a nelineární parametr
rovna 10 rad.s-1, amplituda budící síly A proměnlivá od 0 N do 64 N a nelineární parametr  , pokud nebude nulový, bude roven 4.8.
, pokud nebude nulový, bude roven 4.8.
Biffi a0 64 (c0.1m0.2l0.15s3.9omg10)
 | Bifurkační diagram pro čtyři systémy. Parametr A proměnlivý v rozsahu 0 N až 64 N. Každá ze zobrazených křivek náleží jinému systému. Černá je pro lineární systém, červená pro námi zkoumaný fyzikálně i geometricky nelineární systém, zelená pro pouze geometricky nelineární a modrá pro pouze fyzikálně nelineární systém. Z obrázku je patrno, že při nízkých energiích mají systémy podobné chování, ale fyzikální nelinearita brzy odkloní křivky od lineárního řešení. Geometrická nelinearita způsobí až později odklon způsobem, kterého jsme si všimli již v předchozí části právě při přechodu lineárního chování. Je zde vidět zřetelné zvednutí nad přímku. Dále je patrné, že větší bohatost na nelineární jevy mají systémy s fyzikální nelinearitou, čehož jsme byli svědky i při nižším nelineárním součiniteli  . . |
Fexfi a0 64 (c0.1m0.2l0.15s3.9omg10)
 | Funkce extrému úhlové výchylky  . Parametr A proměnlivý stejně jako v předchozím obrázku. Konvence barev i měřítko osy amplitudy budící síly také stejné. Geometrická nelinearita evidentně a zcela v souladu s intuicí snižuje výchylku v obou systémech, ve kterých je přítomna. Je vidět, že její vliv postupně vzrůstá, i když v případech s fyzikální nelinearitou má menší vliv než by se dalo očekávat. Z obrázku je vidět, že absolutní extrémní výchylka navzdory ustálené výchylce u nelineárních systémů, nepřekročí abso-lutní extrém lineárního systému. . Parametr A proměnlivý stejně jako v předchozím obrázku. Konvence barev i měřítko osy amplitudy budící síly také stejné. Geometrická nelinearita evidentně a zcela v souladu s intuicí snižuje výchylku v obou systémech, ve kterých je přítomna. Je vidět, že její vliv postupně vzrůstá, i když v případech s fyzikální nelinearitou má menší vliv než by se dalo očekávat. Z obrázku je vidět, že absolutní extrémní výchylka navzdory ustálené výchylce u nelineárních systémů, nepřekročí abso-lutní extrém lineárního systému. |
Závěrem:
Poznali jsme, že s velikostí fyzikálně nelineárního členu klesá význam geometrické nelinearity. Ze vzhledu funkcí s fyzikální nelinearitou lze usoudit, že bychom mohli geometrickou nelinearitu dlouho zanedbávat. Až při amplitudě budící síly A rovné 60 N se projeví nějaké významnější odchylky v obou funkcích.
Je zřejmé, že význam geometrické nelinearity souvisí nejen s velikostí fyzikální nelinearity, ale i s funkcí představující fyzikální nelinearitu. Tento fakt vlastně vznikl již s experimenty, na základě kterých jsme diferenciální rovnici sestavili. Totiž, fyzikálně nelineární člen není přímou charakteristikou vlastností pružiny. Je to pouze pokus vyjádřit zjednodušeně fakt, že měření na konstrukci na takovou náhradu ukazuje.
Klíč k tomuto problému může přinést pouze dynamické modelování konstrukce v dalším přiblížení. Představuje to pokus odstranit předpoklady, které jsme pro modelování použili (jediný neohebný nehmotný závěsný prut, soustředění hmoty v jediném hmotném bodu). Jelikož modelování systému s pouhým jedním stupněm volnosti a třemi stavovými proměnnými v současnosti vyžaduje vysoké nároky na výpočetní techniku je takový model otázkou budoucnosti.
Tento závěr bude navazovat na dílčí závěry v jednotlivých experimentech. Aby byl přehledný, bude uspořádán s odrážkami.
Nelineární jevy se objevují již při poměrně nízkých energiích. Jejich projevy jsou stabilní v tom smyslu, že se systém nevyvíjí chaoticky a ani bazény přitažlivosti nemají zpočátku členitější okraj. Teprve později, s narůstající energií, se začíná okraj bazénů členit.
K tomu, aby výrazné nelineární jevy vznikaly, stačí pouze přítomnost kteréhokoliv nelineárního členu v diferenciální rovnici. Avšak člen fyzikální nelinearity může mít vliv na vznik těchto jevů dle své velikosti větší.
Chaotické chování se objevilo až při několikanásobném zvětšení parametru fyzikální nelinearity a při extrémní výchylce poměrně velké. To ukazuje na stabilnost systému, vzhledem k vzniku chaotického chování.
Tlumení se ukázalo jako velmi důležitým členem diferenciální rovnice. Jeho velikost ovlivňuje vznik chaotického chování (čím větší tlumení, tím vyšší hranice energie potřebná k dosažení chaotického chování). Tento fakt však může být ovlivněn tím, že jsme použili útlum lineární. Bylo by vhodné provést praktické měření vlastností útlumu. Útlum také ovlivnil řešitelnost úlohy, protože bez jeho přítomnosti by systém nebyl disipativní, což by řešení značně ztížilo.
Rezonance je další výraznou odlišností od lineárního systému. Jednou z odlišností je existence více limitních cyklů při rezonanci, což může být přínosem. Druhou odlišností je průběh trajektorie při přibližování se k limitnímu cyklu v rezonanci, kdy absolutní extrémní výchylka výrazně přesáhne ustálenou (vliv počátečních podmínek však nebyl detailněji zkoumán). Třetí odlišností je výskyt vedlejších rezonancí, které se vyskytují i ve funkcích extrému výchylky s proměnlivým parametrem amplitudy budící síly A.
Ze simulace vyplynulo, že nelinearita může být pro napjatost konstrukce výhodná. Ovšem její přítomností vzniká možnost vzniku chaotického chování.
Chaotické chování, tak jak jsme ho viděli, bylo ve své podobě poměrně dobře inženýrsky podchytitelné. Jeho projevy byly uzavřené a tedy projekčně použitelné. Útvary, které vznikaly měly zřetelný fraktální tvar.
U systému pouze geometricky nelineárního se chaotické chování objevuje zřejmě až při překročení námi stanovené hranice extrémní výchylky. Tuto hypotézu, která může být pravidlem, by bylo vhodné prokázat.
Pro praktický význam této práce je potřeba provést mnoho experimentů na skutečné konstrukci. Mohlo by to potvrdit či vyvrátit pozorované jevy na našem jednoduchém modelu. Bylo by také třeba zjistit vlastnosti skutečného útlumu.
5. Literatura a ostatní zdroje
Uspořádání zdrojů je provedeno tak, jaký vliv měly na vypracování práce. Čím nižší pořadové číslo, tím vyšší byla pro mě důležitost zdroje pro vypracování.
[1] RNDr. Jiří Macur, CSc., Úvod do teorie dynamických systémů a jejich simulace, 1. vyd., VUT v Brně, PC-DIR, spol. s r.o. - Nakladatelství Brno, prosinec 1995
[2] Prof. Tomasz Kapitaniak, Chaos for Engineers: theory, applications, and control, Springer-Verlag, Heidelberg, 1998
[3] James Gleick, Chaos: vznik nové vědy, Ando Publishing, Brno, 1996
4] John D. Barrow, Teorie všeho, 1. vyd., Mladá fronta, tisk FINIDR, s. r. o., Český Těšín, Praha, 1999
[5] Iain G. Main, Kmity a vlny ve fyzice, 1. vyd., Academia Praha 1990, TISK, n. p., Brno
[6] Programový systém FRACTINT Version 19.6, freeware
Porovnání bylo provedeno na jednotlivých zařízeních pomocí harmonické řady. Výkon daného zařízení a programovacího jazyka je tedy dán množstvím členů řady sečtených za sekundu.

Protože problematika zobrazení vyžaduje řadu speciálních nástrojů, bylo vytvořeno pět souborů se zdrojovými kódy. Tyto soubory jsem rozdělil na hlavní a vedlejší, přičemž hlavní obsahují vlastní simulační procedury.
Hlavní zdrojový kód
{$N+}
Program Trajekt;
Uses Crt,Graph;
Var
grdi,gmi,erri,ki:integer;
cgs:string;
fi,omega,theta:double;
fi0,omega0,theta0:double;
h,h2,pi2:double;
alfa,s,c,m,l,gt,A,omg:double;
T,G,K,P:double;
kx,ky,px,py:real;
exfi,lexfi:double;
flashthetab,flashfib:boolean;
{Rozsirujici funkce}
{$I Tools}
{$I Input}
{$I 3BMP6448}
{****************************************************************************}
{Soustava diferencialnich rovnic systemu}
Function F1(x1,x2,x3:double):double;
begin
F1:=x2;
end;
Function F2(x1,x2,x3:double):double;
begin
{ F2:=-0.5*x2-1*x1+cos(x3);}
F2:=-T*x2-(1+alfa*x1*x1)*K*x1+(G+P*cos(x3))*cos(x1);
{ F2:=-T*x2-K*(1+alfa*x1*x1)*x1+(G+P*cos(x3));}
end;
Function F3(x1,x2,x3:double):double;
begin
F3:=omg;
end;
{Konec soustavy}
{****************************************************************************}
{****************************************************************************}
{Numericke metody}
{Eulerova}
Procedure StepE;
begin
fi:=fi+h*f1(fi,omega,theta);;
omega:=omega+h*f2(fi,omega,theta);
theta:=theta+h*f3(fi,omega,theta);
end;
{Klasicka Runge-Kuttova}
Procedure StepRK(ustavb:boolean);
var k11,k12,k13,k21,k22,k23,k31,k32,k33,k41,k42,k43,ofi:double;
begin
ofi:=fi;
{}
k11:=f1(fi,omega,theta);
k12:=f2(fi,omega,theta);
k13:=f3(fi,omega,theta);
{}
k21:=f1(fi+h2*k11,omega+h2*k12,theta+h2*k13);
k22:=f2(fi+h2*k11,omega+h2*k12,theta+h2*k13);
k23:=f3(fi+h2*k11,omega+h2*k12,theta+h2*k13);
{}
k31:=f1(fi+h2*k21,omega+h2*k22,theta+h2*k23);
k32:=f2(fi+h2*k21,omega+h2*k22,theta+h2*k23);
k33:=f3(fi+h2*k21,omega+h2*k22,theta+h2*k23);
{}
k41:=f1(fi+h*k31,omega+h*k32,theta+h*k33);
k42:=f2(fi+h*k31,omega+h*k32,theta+h*k33);
k43:=f3(fi+h*k31,omega+h*k32,theta+h*k33);
{}
fi:=fi+h/6*(k11+2*k21+2*k31+k41);
omega:=omega+h/6*(k12+2*k22+2*k32+k42);
theta:=theta+h/6*(k13+2*k23+2*k33+k43);
{Ustaveni}
if ustavb then begin
if theta>Pi2 then begin
theta:=theta-Pi2;
flashthetab:=true;
end;
if ((fi>0) and (ofi<0)) or ((fi<0) and (ofi>0)) then begin
flashfib:=true;
end;
end;
if exfi0) then Line(0,Zy(0),639,Zy(0));
if (myd<0) and (myh>0) then Line(Zx(0),0,Zx(0),479);
{Oprava mezi pro pravidelnost deleni}
mxd:=Trunc(mxd/dx)*dx;
myd:=Trunc(myd/dy)*dy;
{Cyklus popisu osy x}
r:=mxd;
repeat
Line(Zx(r),480-4,Zx(r),480);
OutTextXY(Zx(r)+3,480-13,Fix(r,cxi,sxi));
r:=r+dx;
until r>mxh;
{Cyklus popisu osy y}
r:=myd;
repeat
Line(0,Zy(r),4,Zy(r));
OutTextXY(3,Zy(r)-10,Fix(r,cyi,syi));
r:=r+dy;
until r>myh;
end;
{Smazani a sestaveni vzhledu obrazovky}
Procedure gCls(dx,dy:real;cxi,cyi:integer);
begin
ClearDevice;
SetColor(lightgray);
Rectangle(0,0,639,479);
SetColor(lightgray);
Osy(dx,dy,cxi,cyi);
SetColor(white);
end;
{Klavesova nabidka}
Function Menu(ki:integer):integer;
begin
if (ki>0) and (ki<>27) and (ki<>32) then begin
if ki=8 then begin
lexfi:=0;
end
else if (ki=13) or (ki=9) then begin
if ki=9 then begin
Info;
ki:=290;
lexfi:=0;
end;
SaveOb;
end
else if (ki=ord('i')) or (ki=ord('I')) then begin
Info;
end
else if (ki=ord('p')) or (ki=ord('P')) then begin
{ omg:=omg+0.01;}
A:=A+0.1;
Substit;
end
else begin
if ki=1 then begin
ky:=ky*1.1;
py:=py*1.1;
end
else if ki=2 then begin
ky:=ky/1.1;
py:=py/1.1;
end
else if ki=3 then begin
kx:=kx/1.1;
px:=px/1.1;
end
else if ki=4 then begin
kx:=kx*1.1;
px:=px*1.1;
end
else if (ki=ord('a')) or (ki=ord('A')) then begin
px:=px-10;
end
else if (ki=ord('d')) or (ki=ord('D')) then begin
px:=px+10;
end
else if (ki=ord('w')) or (ki=ord('W')) then begin
py:=py-10;
end
else if (ki=ord('s')) or (ki=ord('S')) then begin
py:=py+10;
end;
ki:=290;
end;
end;
Menu:=ki;
end;
{Konec zakladnich funkci}
{****************************************************************************}
{Zobrazi trajektorii systemu}
Procedure ShowTraj;
var xi,yi:integer;
begin
{Pocatecni bod}
xi:=Zx(fi);
yi:=Zy(omega);
{Kontrola zobrazitelnosti}
if (xi>1) and (yi>1) and (xi<640) and (yi<480) then begin
{Nastaveni aktualni pozice}
MoveTo(xi,yi);
{Dalsi krok reseni}
StepRK(true);
{Koncovy bod}
xi:=Zx(fi);
yi:=Zy(omega);
{Kontrola zobrazitelnosti a zobrazeni casti trajektorie}
if (xi>1) and (yi>1) and (xi<640) and (yi<480) then LineTo(xi,yi);
end
else begin
{Dalsi krok reseni}
StepRK(true);
end;
{}
{Dotaz na dosazeni rezne roviny}
if flashthetab then begin
Info;
{Ustaveni promenne rezu}
flashthetab:=false;
end;
end;
{Zobrazi nebo ulozi trajektorii systemu}
Procedure ShowVych(saveb:boolean);
var
xi,yi,ili:integer;
ft:text;
begin
{Podminka pro ulozeni}
if not saveb then begin
{Pocatecni bod}
xi:=Zx(theta);
yi:=Zy(fi);
{ontrola zobrazitelnosti}
if (xi>1) and (yi>1) and (xi<640) and (yi<480) then begin
{Nastaveni aktualni pozice}
MoveTo(xi,yi);
{Dalsi krok reseni}
StepRK(true);
{Koncovy bod}
xi:=Zx(theta);
yi:=Zy(fi);
{Kontrola zobrazitelnosti a zobrazeni}
if (xi>1) and (yi>1) and (xi<640) and (yi<480) then LineTo(xi,yi);
end
else begin
{Dalsi krok reseni}
StepRK(true);
end;
end
else begin {ulozeni}
Assign(ft,'e:\zasobnik.txt');
Append(ft);
WriteLn(ft,fi);
WriteLn(ft,omega);
WriteLn(ft,theta);
Close(ft);
{ for ili:=1 to 10 do StepRK(false);}
for ili:=1 to 10 do StepRK(true);
end;
end;
{Zobrazi rez trajektorii systemu}
Procedure ShowPoin;
begin
{Dalsi krok reseni}
StepRK(true);
{Dotaz na dosazeni rezne roviny}
if flashthetab then begin
{Zobrazeni bodu}
PutPixel(Zx(fi),Zy(omega),15);
Info;
{Ustaveni promenne rezu}
flashthetab:=false;
end;
end;
{Zobrazi zavislost stavove promenne na volenem parametru}
Procedure ShowBif;
var
r:double;
il,itl,bl:longint;
ki:integer;
begin
Init(10,400,-320,239);
gCls(10,0.5,0,1);
{Parametry vykresleni}
itl:=500000; {300000}
bl:=10; {50}
{r:=0.1;}
r:=0.1;
repeat
A:=r;
Init(10,400,-320,239);
PutPixel(Zx(r),Zy(0),black);
for il:=1 to itl do begin
StepRK(true);
PutPixel(0,0,0);
if Menu(Key)=27 then halt;
end;
flashthetab:=false;
il:=1;
repeat
StepRK(true);
if flashthetab then begin
if GetPixel(Zx(r),Zy(fi))<>3 then begin
SaveBod(Zx(r),Zy(fi),0,1);
PutPixel(Zx(r),Zy(fi),3);
end;
flashthetab:=false;
il:=il+1;
end;
PutPixel(0,0,0);
if Menu(Key)=27 then halt;
until il>bl;
r:=r+0.1;
until r>64-0.1;
end;
{Zobrazi extremu stavove promenne na volenem parametru}
Procedure ShowFEx;
var
r:double;
il,itl,bl:longint;
ki:integer;
begin
Init(10,300,-320,239);
gCls(10,0.5,0,1);
{Parametry vykresleni}
itl:=300000; {300000}
bl:=4; {4}
{r:=0.025}
r:=0.1;
repeat
A:=r;
{ omg:=r;}
Init(10,300,-320,239);
PutPixel(Zx(r),Zy(0),black);
for il:=1 to itl do begin
StepRK(true);
PutPixel(0,0,0);
if Menu(Key)=27 then halt;
end;
flashthetab:=false;
lexfi:=0;
il:=1;
repeat
StepRK(true);
if flashthetab then begin
flashthetab:=false;
il:=il+1;
end;
PutPixel(0,0,0);
if Menu(Key)=27 then halt;
until il>bl;
SaveBod(Zx(r),Zy(exfi),0,1);
PutPixel(Zx(r),Zy(exfi),3);
SaveBod(Zx(r),Zy(lexfi),0,1);
PutPixel(Zx(r),Zy(lexfi),3);
r:=r+0.1;
until r>64-0.1;
end;
{Zobrazi aproximace extremni vychylky na volenem parametru}
Procedure ShowSpek;
var
r:double;
i,mi:longint;
k,pc:integer;
begin
pc:=1;
mi:=1000;
repeat
pc:=pc+1;
r:=10;
repeat
omg:=r;
Init(1,1,0,0);
i:=1;
repeat
StepRK(true);
putpixel(0,0,0);
k:=key;
if k=27 then halt;
i:=i+1;
until (i>mi) or (k=13);
PutPixel(Round((r-10)*32),479-Round((exfi-1.3)*1000),pc mod 14+1);
SaveBod(Round((r-10)*32),Round((exfi-1.3)*1000),pc,20);
r:=r+0.03125;
until (r>30) or (k=13);
mi:=Trunc(mi*1.3);
until false;
end;
{****************************************************************************}
{Pocita analyticky linearni oscilator (kontrola)}
Procedure Analyt;
var
t,omn,omd,A1,A2,al,U,Uo,psi,r:real;
xi,yi,ili:integer;
{Inicializace}
Procedure InitAn;
begin
{pomocne promenne}
omn:=sqrt(s/m);
r:=omg/omn;
omd:=omn*sqrt(1-psi*psi);
Uo:=A/s;
U:=Uo/sqrt(Moc(1-r*r,2)+Moc(2*psi*r,2));
if r=1 then al:=PI/2 else al:=arctan(2*psi*r/(1-r*r));
{Integracni konstanty}
A1:=-U*cos(-al);
A2:=1/omd*(omg*U*sin(-al)+A1*psi*omn);
end;
{Vypocet dalsiho stavu}
Procedure StepAn;
begin
fi:=U*cos(omg*t-al)+exp(-psi*omn*t)*(A1*cos(omd*t)+A2*sin(omd*t));
omega:=-omg*U*sin(omg*t-al)+exp(-psi*omn*t)*((A2*omd-A1*psi*omn)*cos(omd*t)-(A1*omd+A2*psi*omn)*sin(omd*t));
end;
begin
psi:=0.0;
s:=1;
m:=1;
A:=1;
omg:=0;
h:=0.1; {h:=0.001}
{}
InitAn;
{}
WriteLn('omn: ',omn);
WriteLn('r: ',r);
WriteLn('omd: ',omd);
WriteLn('Uo: ',Uo);
WriteLn('U: ',U);
WriteLn('al: ',al);
WriteLn('A1: ',A1);
WriteLn('A2: ',A2);
get;
{}
t:=0;
repeat
xi:=Zx(fi);
yi:=Zy(omega);
PutPixel(xi,yi,white);
StepAn;
ki:=Menu(key);
if ki=290 then begin
t:=0;
gCls(0.5,20,1,0);
end;
t:=t+h;
until ki=27;
{}
ClearDevice;
{Vykresleni souradneho krize}
Line(0,trunc(479-2*200),640,trunc(479-2*200));
Line(trunc(1*300),0,trunc(1*300),480);
{cyklus budici frekvence}
omg:=0;
repeat
InitAn;
{cyklus iteraci}
t:=0;
exfi:=0;
for ili:=1 to 20000 do begin
if exfi2.25;
{konec cyklu frekvence}
get;
halt;
end;
{Konec kontroly}
{****************************************************************************}
{****************************************************************************}
Begin
{Pomocna promenna}
pi2:=2*PI;
{Pocatecni podminky}
fi0:=0; {0.3, 0.0749}
omega0:=0;
theta0:=0;
{Parametry}
c:=0.1; {0.1}
m:=0.2; {0.2 kg}
l:=0.15; {0.15 m}
alfa:=0; {0.8*6} {alfa0.8: klidova poloha fi 0.0749}
s:=3.9; {3.9}
gt:=9.81; {9.81 m/s2}
A:=109; {120,145 N}
omg:=10; {10} {A1: subrez 14.95, rez 32.33, A15 rez 42.96 ,A145: rezonance 120.002, exfi 2.4526}
{Krok metod}
h:=0.0001; {0.0001}
{}
{cesta ke grafickemu driveru}
cgs:='E:\TP7\BGI';
{textovy uvod}
ClrScr;
TextColor(green);
WriteLn('Program SimNelK');
TextColor(lightgray);
WriteLn('Autor '+Autor+', rok emise 2000.');
WriteLn('(Program pro simulaci disipativniho dynamickeho systemu)');
WriteLn;
Writeln(' Esc - ukonceni');
WriteLn(' Enter - ulozeni');
WriteLn(' Sipky - zoom');
WriteLn(' A,W,S,D - posun os');
WriteLn(' I - informacni okenko');
WriteLn(' P - dana zmena daneho parametru');
WriteLn(' Mezera - restart simulace');
WriteLn('BackSpace - vynulovani znacky lokalni extremni vychylky');
WriteLn(' Tab - ulozeni a vymazani obrazovky');
WriteLn;
TextColor(white);
WriteLn('(Stiskni klavesu)');
WriteLn;
TextColor(lightgray);
if Get<>27 then begin
{Inicializace grafiky}
grdi:=Detect;
InitGraph(grdi,gmi,cgs);
erri:=GraphResult;
if erri=GrOK then begin
{Pauza pro grafiku}
Delay(1000);
SetFillStyle(1,7);
{ ShowSpek;
halt;
{ ShowBif;
halt;}
{ ShowFEx;
halt;}
Init(Moc(1.1,70),Moc(1.1,4),0,0);
{ Init(Moc(1.1,90),Moc(1.1,50),0,0);}
{cyklus pripadu}
repeat
Restart;
gCls(0.5,20,1,0);
{ gCls(0.1,1,1,0);}
MoveTo(Round(320+px),240);
{ Analyt;}
{cyklus simulace}
repeat
{ ShowVych(true);}
ShowPoin;
{ ShowTraj;}
PutPixel(0,0,0); {akce, problem Windows}
ki:=Menu(Key);
if ki=290 then gCls(0.5,20,1,0);
{ if ki=290 then gCls(0.1,1,1,0);}
until (ki=32) or (ki=27);
{konec cyklu simulace}
until ki=27;
{konec cyklu pripadu}
{Uzavreni grafiky}
CloseGraph;
Delay(1000);
end
else begin
WriteLn('Chyba grafiky: ',GraphErrorMsg(erri));
end;
end;
ClrScr;
end.
#include (math.h)
#include (stdio.h)
#include (conio.h)
#include (stdlib.h)
#include (fcntl.h)
#include (sys\stat.h)
#include (io.h)
#define pi 3.14159265358979323846
double T,G,K,P;
double fi,omega,theta;
int flashtheta;
double pi2=2*pi;
double fi0=0; //0.3
double omega0=0;
double theta0=0;
double c=0.1; //0.1 kg/s
double m=0.2; //0.2 kg
double l=0.15; //0.15 m
double alfa=0.8; //0.8*6
double s=3.9; //3.9
double gt=9.81; //9.81 m/s2
double A=1; //72.8,11.5,120,145 N
double omg=32.34; //10 A145: rezonance 120.002, exfi 2.4526
double h=0.0001; //0.0001
double h2=0.5*h;
//Numericke metody
void steprk()
{
#define f1(x1,x2,x3) x2
#define f2(x1,x2,x3) -T*(x2)-(1+alfa*(x1)*(x1))*K*(x1)+(G+P*cos(x3))*cos(x1)
#define f3(x1,x2,x3) omg
double k11=f1(fi,omega,theta);
double k12=f2(fi,omega,theta);
double k13=f3(fi,omega,theta);
double k21=f1(fi+h2*k11,omega+h2*k12,theta+h2*k13);
double k22=f2(fi+h2*k11,omega+h2*k12,theta+h2*k13);
double k23=f3(fi+h2*k11,omega+h2*k12,theta+h2*k13);
double k31=f1(fi+h2*k21,omega+h2*k22,theta+h2*k23);
double k32=f2(fi+h2*k21,omega+h2*k22,theta+h2*k23);
double k33=f3(fi+h2*k21,omega+h2*k22,theta+h2*k23);
double k41=f1(fi+h*k31,omega+h*k32,theta+h*k33);
double k42=f2(fi+h*k31,omega+h*k32,theta+h*k33);
double k43=f3(fi+h*k31,omega+h*k32,theta+h*k33);
fi+=h/6*(k11+2*k21+2*k31+k41);
omega+=h/6*(k12+2*k22+2*k32+k42);
theta+=h/6*(k13+2*k23+2*k33+k43);
//Ustaveni
if (theta>pi2)
{
theta-=pi2;
flashtheta=1;
}
else
{
flashtheta=0;
}
}
//Vynulovani casu systemu
void restart()
{
//Pocatecni podminky
fi=fi0;
omega=omega0;
theta=theta0;
}
//Inicializace promennych
void init()
{
restart();
//Koeficienty pro snizeni poctu parametru
T=c/m;
G=gt/l;
K=s/m/l/l;
P=A/m/l;
}
//Pocita oblasti pritazlivosti
void main()
{
double mfid=-1.5;
double momegad=-50;
double mfih=1.5;
double momegah=50;
double nfi=128;
double nomega=96;
double dfi=(mfih-mfid)/nfi;
double domega=(momegah-momegad)/nomega;
int iti,fb;
int handle;
//Otevreni souboru
handle=open("Out.num",O_WRONLY | O_CREAT | O_TRUNC | O_BINARY,S_IREAD | S_IWRITE);
printf("Spusten modul BazPrit\n");
printf("=====================\n");
omega0=momegad+domega*51;
while(omega0<=momegah)
{
fi0=mfid;
while(fi0<=mfih)
{
init();
printf("fi0=%18.12f\n",fi0);
printf("omega0=%18.12f\n",omega0);
iti=1;
while(iti<=170)
{
flashtheta=0;
while(flashtheta==0)
{
steprk();
if(kbhit()) return;
}
iti++;
}
write(handle,&fi0,8);
write(handle,&omega0,8);
write(handle,&fi,8);
printf("finek=%18.12f (%3d)\n",fi,iti-1);
fi0+=dfi;
}
omega0+=domega;
}
//Zavreni souboru
close(handle);
}
Vedlejší zdrojové kódy
Zobrdou.pas (grafické zobrazení vypočtených dat pro program Bazprit)
Printdou.pas (textové zobrazení vypočtených dat pro program Bazprit)
Frp.lsp (program pro převod dat do programu AutoCAD)

Obrázek ze statického měření průhybu konzoly z pružinové oceli. Konzola se záměrnými body je vzadu. Měřící aparatura v popředí.

Obrázek konzoly při zatížení.
Tabulka naměřených hodnot, jejich přepočet a hodnoty aproximace.