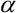= 0.8, lineární tuhost s = 3.4 N.m.rad-1, konstanta útlumu c = 0.1 N.m-1.s.
Abstract
The dynamic non-linear solution of the harmonic loaded structure is analysed. The cantilever beam is modelled as the system with one degree of freedom with linear dumping decrement. Problem is solved with variable parameters and solution is focused on searching of non-linear phenomena near small and/or large deformations.
Úvod
Zkoumaný problém je dynamické nelineární řešení konstrukce zatížené harmonickým zatížením. Konstrukce představuje konzolový nosník modelovaný soustavou s jedním stupněm volnosti s lineárním útlumem. Řešení je provedeno pro proměnné parametry a je zaměřeno na hledání nelineárních jevů při malých i velkých deformacích a pro parametry zjištěné na skutečné konstrukci i pro parametry fiktivní.
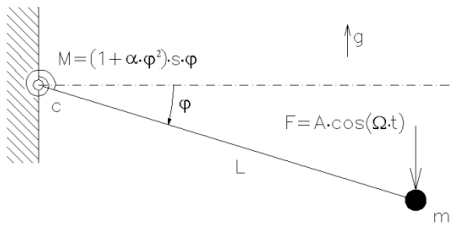
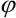úhlová výchylka, 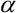nelineární koeficient, s lineární tuhost pružiny, c konstanta útlumu, L délka závěsného prutu, m hmotnost hmotného bodu, g tíhové zrychlení, A amplituda budící síly, 
budící frekvence a t čas.
Hodnoty parametrů modelu
Konstrukce, která je modelována, byla sestrojena a staticky zatěžována. Nosník byl z ploché pružinové oceli, schopné velkých pružných deformací. Byla zjištěna nelineární závislost momentu ve vetknutí M na pootočení j koncového bodu, viz obr. 2. Tato vlastnost je v modelu zohledněna pomocí aproximace naměřených hodnot neúplným polynomem třetího stupně s nenulovým lineárním a kubickým členem, viz obr. 1 (jsou vybrány tyto dva členy, protože pouze tak je funkce symetrická k počátku, což nám zajišťuje nezávislost na směru zatěžování).
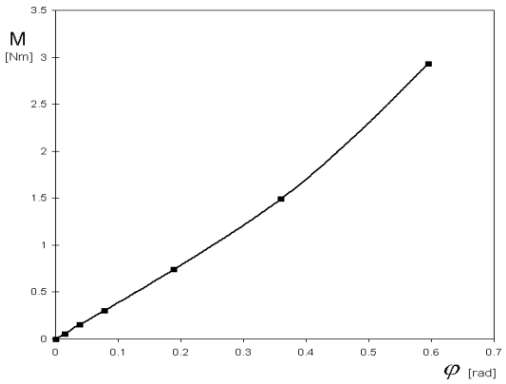
. Aproximace této funkce je dle obr. 1 s parametry nelineárním součinitelem = 0.8 a lineární tuhostí s = 3.4 N.m.rad-1.
Všechny hodnoty konstukčních parametrů jsou: hmotnost hmotného bodu m = 0.2 kg, délka závěsného prutu L = 0.15 m, nelineární součinitel = 0.8, lineární tuhost s = 3.4 N.m.rad-1, konstanta útlumu c = 0.1 N.m-1.s.
Protože konstrukce nebyla měřena dynamicky, byl parametr útlumu pouze odhadnut.
Matematický model
Podle obr. 1 můžeme sestavit diferenciální rovnici dynamické rovnováhy. Výsledný tvar po úpravách lze psát takto:
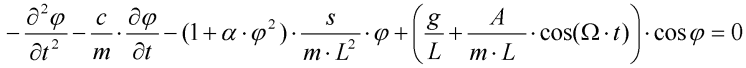
Pomocí substitucí
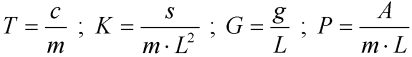
lze zápis zjednodušit na:
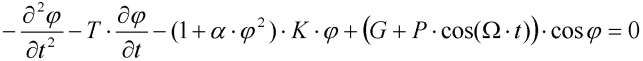
Zavedením stavových proměnných úhlová rychlost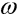 
a fáze budící síly 
, pro něž lze psát:
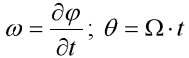
dostáváme kanonický tvar soustavy diferenciálních rovnic prvního řádu, což je třeba pro numerické řešení:
Pro řešení této soustavy jsem pro jednoduchost vybral metodu klasickou Runge-Kuttovu, která je jednou ze základních metod numerické matematiky.
Zobrazovací metody
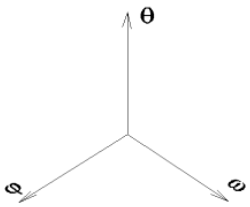
JK zobrazení řešení je potřeba použít zobrazovacích metod, které nejsou v inženýrské praxi obvyklé. Řešení dynamického systému je dobré zobrazit v tzv. fázovém prostoru, jehož každý rozměr je stavová proměnná systému (s výhodou zde máme pouze tři stavové proměnné) viz obr. 3.
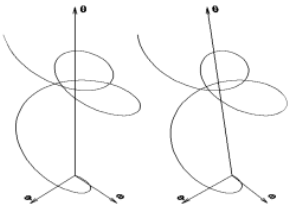
Řešením je ve fázovém prostoru tzv. trajektorie systému viz obr. 4 (v anaglyfové podobě).
Jedno ze zajímavých řešení systému s parametry získanými měřením je na obr. 5. Je to graf dosažené extrémní výchylky v závislosti na změně parametru amplitudy budící síly A. Jsou na něm vidět dvě zvláštní oblasti. Obě oblasti jsou oblastmi nestability systému. Je zde vidět, že obě oblasti jsou oblastmi rezonance.
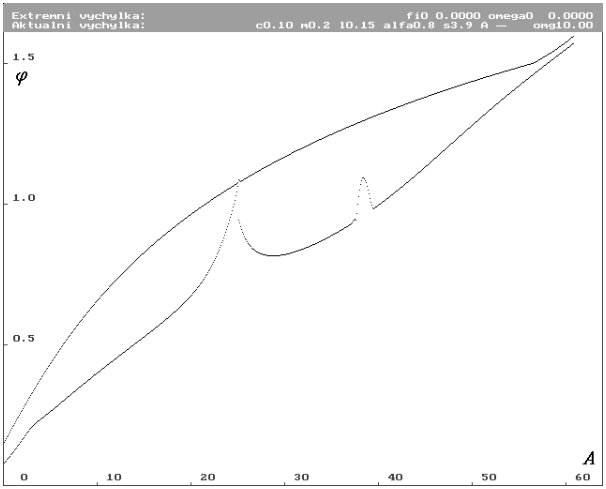
rovný 0.8, frekvence budící síly rovná 10 rad.s-1 a amplitudou budící síly A proměnlivou v rozsahu 0 až 64 N. Horní funkce je absolutní extrémní výchylkou pro zvolené počáteční podmínky a spodní funkce je ustálenou extrémní výchylkou.
Závěr
Na studované konstrukci se při rezonancích objevily významné nelineární jevy až při poměrně velké úhlové výchylce. Podstatné rozdíly mezi lineárním systémem a systémem nelineárním se však objevují již při výchylkách i desetkrát menších, než jaká je vidět u rezonancí na obr. 5. K tomu, aby výrazné nelineární jevy vznikaly, stačí pouze přítomnost kteréhokoliv nelineárního členu v diferenciální rovnici. Avšak člen fyzikální nelinearity může mít vliv na vznik těchto jevů dle své velikosti větší.
Poděkování
Práce na tomto příspěvku byly podporovány z prostředků projektu GA ČR 103/00/0093 a výzkumného záměru CEZ: J22/98: 261100009.
Literatura
[1] Petr Frantík, Chování silně nelineární stavební konstrukce, diplomová práce, VUT v Brně, červen 2000
[2] Jiří Macur, Úvod do teorie dynamických systémů a jejich simulace, 1. vyd., VUT v Brně, PC-DIR, spol. s r.o. - Nakladatelství Brno, prosinec 1995
[3] Iain G. Main, Kmity a vlny ve fyzice, 1. vyd., Academia Praha 1990, TISK, n. p., Brno