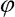 je pootočení prutu
je pootočení prutu
* Ing. Petr Frantík: Ústav stavební mechaniky, Fakulta stavební, Vysoké učení technické v Brně; Veveří 95, 662 37 Brno; e-mail: kitnarf at centrum dot cz
Summary: The strange attractor shape of the nonlinear dynamic one-degree-of-freedom model of harmonic loaded cantilever beam is described in this paper. The change of strange attractor Poincare map topology and its fractal capacity dimension is investigated during the period of the harmonic load.
1. Úvod
Zjednodušeně lze konzolový nosník modelovat jednostupňovým modelem, zobrazeným se svou předlohou na obr. 1. Takový model má několik výhod. Snadno se definuje, řeší a v případě, že je dynamicky zatížený, jej lze užít k rozsáhlým simulacím, což u komplikovanějších modelů klade přílišné nároky na výpočetním čas.
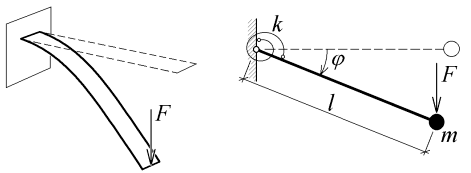
Obr. 1: Konstrukce a její jednostupňový model s označením: F je zatěžující síla, m je náhradní hmotnost prutu, l je délka prutu, k je náhradní tuhostí konstanta prutu a 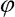 je pootočení prutu
je pootočení prutu
Uvažujme, že je nosník tvořen štíhlým prutem, který umožňuje velké průhyby volného konce při pružném chování materiálu. Tento prut je na obr. 1 nahrazen tuhým nehmotným dílcem upevněným ve vetknutí kloubem s rotační pružinou a soustředěnou hmotou m na jeho konci. Pružina nechť působí na tuhý dílec momentem M o velikosti:
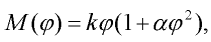 | (1) |
kde 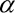 je nelineární součinitel. Dále uvažujme, že nosník je umístěn ve svislém gravitačním poli a dále, že je na volném konci zatížen harmonicky proměnnou silou danou vztahem:
je nelineární součinitel. Dále uvažujme, že nosník je umístěn ve svislém gravitačním poli a dále, že je na volném konci zatížen harmonicky proměnnou silou danou vztahem:
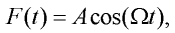 | (2) |
kde t je čas, A je amplituda síly a  je frekvence síly. Pohybové rovnice lze potom psát:
je frekvence síly. Pohybové rovnice lze potom psát:
 | (3) |
kde 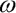 je úhlová rychlost dílce, c je součinitel viskózního útlumu a g je tíhové zrychlení.
je úhlová rychlost dílce, c je součinitel viskózního útlumu a g je tíhové zrychlení.
2. Simulace
Některé vlastnosti vzniklého dynamického systému (3) již byly zkoumány, viz např. (Frantík, 2001). Zde se budeme soustředit na atraktor systému s parametry: náhradní hmotnost m=0.2 kg, délka prutu l=0.15 m, tuhost pružiny k=3.9 N.m.rad-1, tíhové zrychlení g=9.81 m.s-2, parametr tlumení c=0.1 N.s.m-1, frekvence síly  =10 rad.s-1, amplituda síly A=110.3 N. Tento systém řešme numerickou klasickou Runge-Kuttovou metodou s krokem h=0.002 s. Polohu atraktoru si můžeme znázornit bifurkačním diagramem na obr. 2.
=10 rad.s-1, amplituda síly A=110.3 N. Tento systém řešme numerickou klasickou Runge-Kuttovou metodou s krokem h=0.002 s. Polohu atraktoru si můžeme znázornit bifurkačním diagramem na obr. 2.
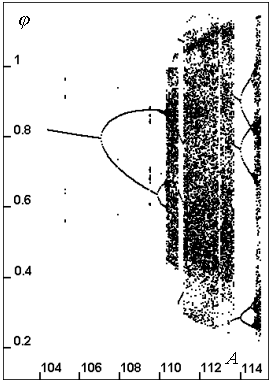 | Obr. 2: Bifurkační diagram pro pootočení 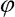 v řezu trajektorií - Poincarého mapě (definice viz (Macur, 1995)); pro vytváření Poincarého mapy platí, že fáze v řezu trajektorií - Poincarého mapě (definice viz (Macur, 1995)); pro vytváření Poincarého mapy platí, že fáze 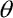 =2 =2 i, i=0, 1, 2,…) a to pro proměnnou amplitudu síly A v intervalu 104 N až 115 N. i, i=0, 1, 2,…) a to pro proměnnou amplitudu síly A v intervalu 104 N až 115 N.
|
V bifurkačním diagramu na obr. 2 můžeme vidět, že do hodnoty amplitudy síly A=107 N existuje jednoduchý limitní cyklus (v Poincarého mapě má jeden bod) a někde těsně za hodnotou A=107 N dochází k postupným bifurkacím až k vybranému chaotickému atraktoru, který má hodnotu amplitudy síly A=110.3 N.
Protože se budeme snažit popsat komplikovaný chaotický atraktor (viz obr. 3b a 4b), ukáže se výhodné srovnat jej s jednoduchým limitním cyklem (viz obr. 3a a 4a) před postupnými bifurkacemi (systém s amplitudou síly A=107 N).
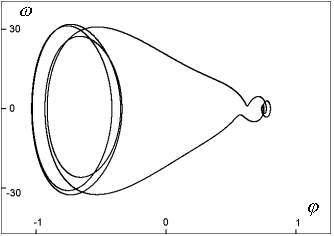 | Obr. 3a: Projekce jednoduchého limitního cyklu do roviny 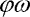 systému s amplitudou síly A=107 N systému s amplitudou síly A=107 N
|
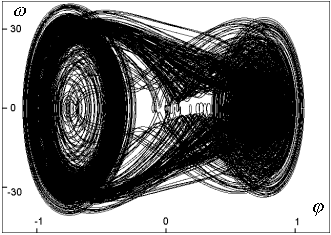 | Obr. 3b: Projekce chaotického atraktoru do roviny 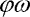 systému s amplitudou budící síly A=110.3 N (trajektorie je omezena) systému s amplitudou budící síly A=110.3 N (trajektorie je omezena)
|
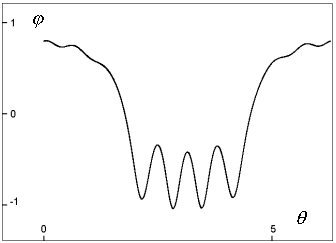 | Obr. 4a: Projekce jednoduchého limitního cyklu do roviny  systému s amplitudou síly A=107 N systému s amplitudou síly A=107 N
|
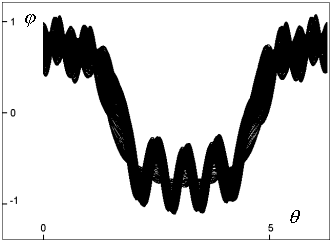 | Obr. 4b: Projekce chaotického atraktoru do roviny  systému s amplitudou budící síly A=110.3 N (trajektorie je omezena) systému s amplitudou budící síly A=110.3 N (trajektorie je omezena)
|
Na obrázcích 3a, 4a jsou dva kolmé průměty jednoduchého limitního cyklu systému s amplitudou A=107 N, což je systém těsně před bodem bifurkace (viz obr. 2). Z obrázků je patrné, že se trajektorie osmkrát ovine za periodu budící síly. Chaotický atraktor systému s amplitudou síly A=110.3 N je obdobně promítnut na obrazcích 3b, 4b. Systém je po mnoha bifurkacích příliš komplikovaný - chaotický, nedochází k ustálení do limitního cyklu.
Provedeme-li řezy - Poincarého mapy v různých úrovních fáze síly 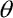 , tj. tak, že pro každou Poincarého mapu bude platit:
, tj. tak, že pro každou Poincarého mapu bude platit:
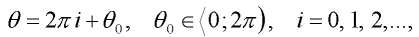 | (4) |
kde 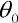 je úroveň fáze síly Poincarého mapy, zjistíme, že se fraktální útvar v Poincarého mapě pouze otáčí, posouvá a deformuje. Nedochází však zřejmě k jeho topologické změně. Na obrázku 5 jsou příklady Poincarého map pro různé úrovně fáze síly.
je úroveň fáze síly Poincarého mapy, zjistíme, že se fraktální útvar v Poincarého mapě pouze otáčí, posouvá a deformuje. Nedochází však zřejmě k jeho topologické změně. Na obrázku 5 jsou příklady Poincarého map pro různé úrovně fáze síly.
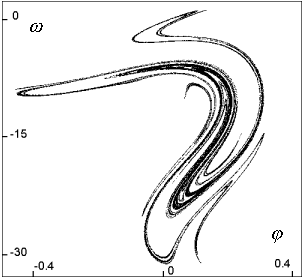
 | Obr. 5a: Poincarého mapa chaotického atraktoru A=110.3 N s úrovní fáze síly 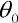 =0 rad; na počátku resp. konci periody síly; poměrně řídká fraktální struktura =0 rad; na počátku resp. konci periody síly; poměrně řídká fraktální struktura
|
 | Obr. 5b: Poincarého mapa chaotického atraktoru A=110.3 N s úrovní fáze síly 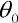 =1.697 rad; čtvrtina periody síly, útvar se rychle přesouvá do záporných hodnot pootočení =1.697 rad; čtvrtina periody síly, útvar se rychle přesouvá do záporných hodnot pootočení 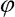 ; topologicky shodný útvar jako na obr. 5a ; topologicky shodný útvar jako na obr. 5a
|
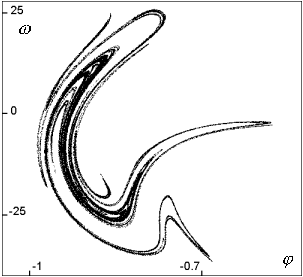 | Obr. 5c: Poincarého mapa chaotického atraktoru A=110.3 N s úrovní fáze síly 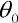 =2.136 rad; útvar se při rotaci v záporných hodnotách pootočení =2.136 rad; útvar se při rotaci v záporných hodnotách pootočení 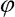 hodně protahuje hodně protahuje
|
 | Obr. 6: Znázornění pohybu útvaru v Poincarého mapě pro systém s amplitudou síly A=110.3 N; sto řezů s ekvidistantní vzdáleností |
Na obrázcích 5a až 5c bylo patrné, že se útvar v Poincarého mapě topologicky nemění. Znázornění pohybu útvaru však v této statické podobě je problémem, protože se útvar celkem osmkrát otočí za periodu síly. Jisté přiblížení lze získat z obrázku 6. Osmero otočení útvaru odpovídá počtu ovinutí trajektorie limitního cyklu před bodem bifurkace (amplituda síly A=107 N), což je povzbudivé.
3. Měření
Topologickou neproměnnost fraktálního útvaru v řezu ověřme měřením fraktální dimenze jednotlivých útvarů. K měření fraktální dimenze útvarů v Poincarého mapách je užita optimalizovaná metoda box-counting s proměnným růstem sítě (Frantík et al., 2002; Frantík et al., 2003.03). Tato metoda měří kapacitní fraktální dimenzi dc, viz např. (Kapitaniak 1998). Výsledné kapacitní dimenze deseti útvarů v ekvidistantně vzdálených řezech jsou zobrazeny na obr. 7.
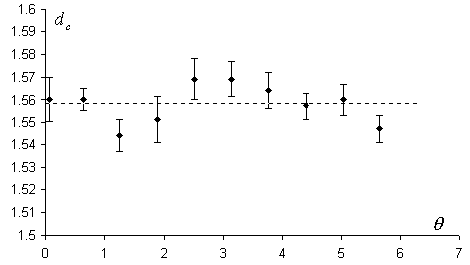 | Obr. 7: Graf naměřených kapacitních dimenzí pro útvary v Poincarého mapách systému A=110.3 N; průměrná hodnota dimenze činí dc=1.558 |
6. Závěr
Prozkoumaný chaotický atraktor dynamického systému, který modeluje harmonicky zatížený konzolový nosník má zajímavé vlastnosti. Ačkoliv je třeba splnit podmínku exponenciálního vzdalování blízkých trajektorií, což je zdrojem chaotického chování, zůstává útvar v Poincarého mapě při jejím libovolném fázovém posunu zřejmě nezměněn. Například u chaotického atraktoru harmonicky zatíženého jednostupňového modelu vzpěru prutu (Frantík 2003.01) tomu tak není. U tohoto podobného systému dochází na útvaru k roztahování a skládání, obdobně jak je tomu u Smaleovy podkovy (Kapitaniak 1998). Na zde popsaném útvaru však takové změny nejsou patrné.
Nemění-li se útvar v průběhu periody lze učinit závěr, že musí být kompaktní (souvislý), aby se trajektorie systému mohla spojitě po útvaru přesouvat, přičemž musí být zachována hustota trajektorií v dané oblasti útvaru (na obr. 6 je vidět, že i hustota trajektorií se na útvaru v průběhu periody síly nemění).
Jednoduchý limitní cyklus před kaskádou bifurkací vedoucích k chaotickému chování se ukázal jako vhodný k ilustraci posunu a otáčení útvaru v Poincarého mapě chaotického atraktoru.
Měření kapacitní fraktální dimenze útvarů ve fázově posunutých Poincarého mapách zkoumaného atraktoru ukazuje na shodu těchto útvarů vzhledem k této dimenzi a dobře doplňuje pozorovanou vizuální totožnost.
Poděkování
Tento příspěvek byl vytvořen v rámci výzkumného záměru CEZ: J22/98: 261100009 a s podporou grantu GA ČR 103/03/1350.
Literatura
Frantík, P. (2001) Sledování a simulace nelineární dynamické konstrukce, 3. odborný seminář doktorského studia, VUT FAST v Brně, Brno
Frantík, P., Keršner, Z., Macur, J. (2002) Estimation of fractal dimension: optimised box-counting method, International symposium Non-Traditional Cement & Concrete, BUT, Brno
Frantík, P. (2003.01) Dynamický jednostupňový model vzpěru prutu: Chaotické chování, seminář Modelování v mechanice 2003, VŠB-TU Ostrava
Frantík, P., Keršner, Z., Stibor, M. (2003.03) Optimised box-counting method: effect of mesh size distribution, sborník k výročí prof. Bittnara, ČVUT Praha
Kapitaniak, T. (1998) Chaos for Engineers: theory, applications and control, Springer-Verlag Berlin
Macur, J. (1995) Úvod do teorie dynamických systémů a jejich simulace, PC-DIR 1995, Brno