Petr Frantík1
1Petr Frantík, Ing., Vysoké učení technické v Brně, Fakulta stavební, Ústav stavební mechaniky, Veveří 95, 662 37 Brno, e-mail: kitnarf at centrum dot cz
Abstrakt: V článku se předkládá odvození vztahu pro příčnou kontrakci nestlačitelného materiálu včetně srovnání s experimentálním měřením. Ukazuje se, že obvykle užívané vztahy nepřesně vystihují reálné chování materiálu. Je navrženo zlepšení užívaných vztahů použitelné alespoň pro přesnější identifikaci materiálových vlastností pružnějších materiálů.
Příčná kontrakce je známa jako jev vznikající při natahování nebo stlačování pružného tělesa, při kterém dochází ke změně rozměrů kolmých ke směru namáhání. Tento jev lze snadno vysvětlit jako snahu materiálu odolávat tendenci ke změně jeho objemu. Za meze lze považovat materiál dokonale nestlačitelný a dokonale stlačitelný, přičemž zřejmě nelze vyloučit existenci materiálu za těmito vytyčenými hranicemi (např. materiál zvyšující svůj objem při stlačování nebo natahování, viz např. [1])
1 Poissonovo číslo 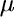
Nejčastěji je jev příčné kontrakce modelován s pomocí koeficientu příčné kontrakce - tzv. Poissonova čísla 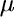 , které je v případě pružné homogenní látky namáhané normálovým zatížením v jednom směru dáno vztahem:
, které je v případě pružné homogenní látky namáhané normálovým zatížením v jednom směru dáno vztahem:
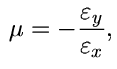 | (1) |
kde 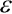 x je poměrné přetvoření elementu ve směru namáhání a
x je poměrné přetvoření elementu ve směru namáhání a 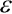 y je poměrné přetvoření elementu ve směru kolmém na směr namáhání. Vztah pro poměrné přetvoření je obvykle ve tvaru:
y je poměrné přetvoření elementu ve směru kolmém na směr namáhání. Vztah pro poměrné přetvoření je obvykle ve tvaru:
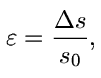 | (2) |
kde s0 je šířka elementu ve zvoleném směru před deformací
a 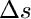 je přírůstek této šířky po deformaci.
je přírůstek této šířky po deformaci.
Poissonovo číslo 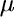 tedy udává míru příčné deformace, jejíž příčinou byla deformace podélná. Uvažuje se pro daný materiál
konstantní hodnotou z intervalu <0,0.5>, přičemž
hodnota 0 odpovídá materiálu dokonale stlačitelnému a hodnota 0.5
materiálu dokonale nestlačitelnému (nověji je dolní mez intervalu
uvažována hodnotou -1, viz [1]). Pokusme se objasnit
hodnotu 0.5 pro nestlačitelný materiál.
tedy udává míru příčné deformace, jejíž příčinou byla deformace podélná. Uvažuje se pro daný materiál
konstantní hodnotou z intervalu <0,0.5>, přičemž
hodnota 0 odpovídá materiálu dokonale stlačitelnému a hodnota 0.5
materiálu dokonale nestlačitelnému (nověji je dolní mez intervalu
uvažována hodnotou -1, viz [1]). Pokusme se objasnit
hodnotu 0.5 pro nestlačitelný materiál.
2 Nestlačitelný materiál
Uvažujme hranol z nestlačitelného pružného homogenního materiálu, který při libovolné změně tvaru zachovává svůj objem, viz obr. 1.
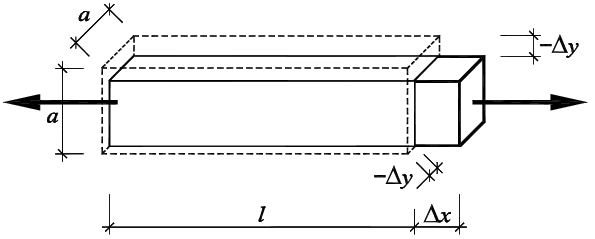
Obrázek 1: Hranol před a po deformaci
Na obr. 1 je znázorněn hranol před deformací a po deformaci způsobené podélným tahem. Z experimentů (viz např. [2]) vyplývá, že čtvercový tvar průřezu zůstává i při velkém protažení hranolu zachován. Odvoďme nyní vztah pro koeficient příčné kontrakce z rovnosti objemů hranolu před a po deformaci. Rovnost objemů lze zapsat vztahem (sledujme obr. 1):
 | (3) |
což můžeme s využitím vztahu (2) upravit:
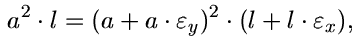 | (4) |
dále uplatněním vztahu (1) včetně úpravy obdržíme:
 | (5) |
z čehož snadno odvodíme, že pro Poissonovo číslo 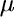 nestlačitelného materiálu platí:
nestlačitelného materiálu platí:
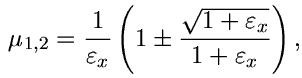 | (6) |
přičemž použitelná hodnota je 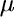 2 (užití záporného znaménka před odmocninou). Můžeme tedy psát:
2 (užití záporného znaménka před odmocninou). Můžeme tedy psát:
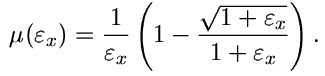 | (7) |
Odvozená závislost (7) je zobrazena na obr. 2. Můžeme vidět, že
konstantní hodnota koeficientu kontrakce je velmi hrubá aproximace
pro oblast větších přetvoření, protože odvozená závislost nemá
nulovu derivaci ani při nulové hodnotě přetvoření 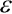 x.
x.
Lze ukázat, že pro nalezenou závislost (7) platí:
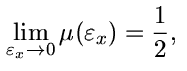 | (8) |
což je běžně užívaná hodnota Poissonova čísla 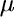 nestlačitelného materiálu.
nestlačitelného materiálu.

Obrázek 2: Průběh závislosti koeficientu příčné kontrakce na poměrném přetvoření
2 Experiment
Ověření zjištěné závislosti bylo provedeno experimentálním měřením
v tahu na hranolu z letecké gumy s čtvercovým průřezem 4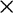 4
mm, měřené délky 143 mm. Srovnání výsledků měření se závislostí
(7) pro nestlačitelný materiál je na obr. 3.
4
mm, měřené délky 143 mm. Srovnání výsledků měření se závislostí
(7) pro nestlačitelný materiál je na obr. 3.
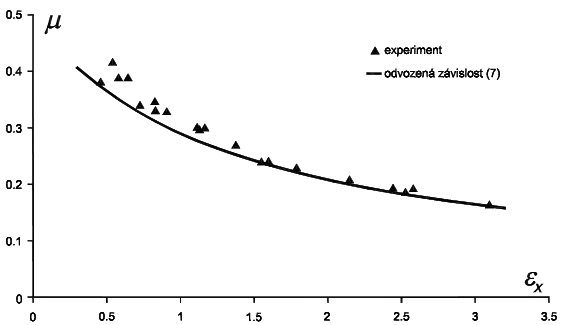
Obrázek 3: Graf srovnání odvozené závislosti s experimentálním měřením
Z grafu na obr. 3 je patrné, že guma odpovídá svým chováním nestlačitelnému materiálu, přičemž se experimentem potvrdil průběh odvozené závislosti (7).
2 Lineární aproximace
Z grafu na obr. 2 je dobře vidět již zmíněný problém s nenulovou derivací odvozené závislosti, který způsobuje nevhodnost konstantní aproximace v oblasti dosahovaných přetvoření. Pro lepší výstižnost popisu tohoto jevu můžeme užít aproximace lineární. Derivaci závislosti (7) lze odvodit do tvaru:
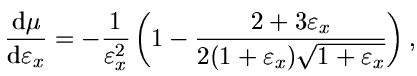 | (9) |
potom pro stanovení směrnice lineární aproximace potřebujeme znát
limitu výrazu (9) pro 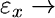 , kterou snadno
vypočteme dvojnásobným užitím L'Hospitalova pravidla:
, kterou snadno
vypočteme dvojnásobným užitím L'Hospitalova pravidla:
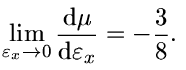 | (10) |
Lineární aproximaci pro nestlačitelný materiál pak můžeme psát ve tvaru:
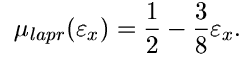 | (11) |
Závěr
Rozbor jevu příčné kontrakce a dobrá shoda nalezené závislosti s experimentálním měřením naznačují problematičnost současného modelování tohoto jevu u materiálů s větším poměrným přetvořením. Na nestlačitelném materiálu bylo ukázáno, že užívaná aproximace příčné kontrakce je z hlediska jí samotné velmi nepřesná i při (pro užitý materiál) nevelkých přetvořeních (chyba této aproximace je větší jak 7% pro 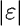 = 0.1). Byla proto navržena aproximace vyššího stupně (konkrétně lineární), která bude mít hlavní význam zřejmě při identifikaci materiálových vlastností pružnějších materiálů.
= 0.1). Byla proto navržena aproximace vyššího stupně (konkrétně lineární), která bude mít hlavní význam zřejmě při identifikaci materiálových vlastností pružnějších materiálů.
Poděkování
Tento příspěvek byl vytvořen v rámci výzkumného záměru CEZ: J22/98: 261100009 a s podporou grantu GA ČR 103/03/1350 a nadace Preciosa.
Literatura
[1] FRISS, E. A.,LAKES, R. S., AND PARK, J. B. Negative Poisson,s ratio polymeric and metallic materials. Journal of Materials Science, 23, 4406 - 4414: 1998.
[2] Frantík, P. Poissonovo číslo (?) cementových kompozitů. VI. komorní seminář Úskalí lomové mechaniky kompozitů na silikátové a jiné bázi, http://www.fce.vutbr.cz/stm/fracture/kseminar/ks06/zprava.htm, VUT FAST v Brně: Brno 2001.