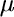 = 0.2, pevnost v tahu Rt = 3.3 MPa, pevnost v tlaku Rc = -36.3 MPa, specifická lomová energie Gf = 6 N/m.
= 0.2, pevnost v tahu Rt = 3.3 MPa, pevnost v tlaku Rc = -36.3 MPa, specifická lomová energie Gf = 6 N/m.| MODELOVÁNÍ V MECHANICE | ÚNOR, OSTRAVA 2005 |
1Petr Frantík, Ing., Ph.D., Vysoké učení technické v Brně, Fakulta stavební, Ústav stavební mechaniky, Veveří 95/331, 602 00 Brno, e-mail: kitnarf at centrum dot cz
2Zbyněk Keršner, Ing., CSc, Vysoké učení technické v Brně, Fakulta stavební, Ústav stavební mechaniky, Veveří 95/331, 602 00 Brno, e-mail: kersner.z at fce.vutbr dot cz
3Patrik Štancl, Ing., Vysoké učení technické v Brně, Fakulta stavební, Ústav stavební mechaniky, Veveří 95/331, 602 00 Brno,
e-mail: patrik.stancl at tobrys dot cz
Abstrakt: The influence of different boundary conditions in numerical modelling of compression test of specimen of quasibrittle material is studied in this paper.
1 Úvod, tlakové porušení
V rámci výzkumu porušování cementových kompozitů namáhaných vysokými teplotami se hodnotí výsledky dvou typů zatěžovacích zkoušek vzorků z jednoho druhu cementové malty. Potřeba srovnání výsledků zkoušek souvisí s možností využití tlakových experimentů, prováděných Ing. Ditou Matesovou na Northwestern University v centru ACBM, k určení lomových charakteristik vyšetřovaných kvazikřehkých kompozitů. Pro úspěšné navázání výzkumu je zapotřebí porozumět souvislostem mezi chováním zkušebních vzorků ze zmíněných materiálů při porušení tlakem a při porušení u tradiční konfigurace lomového experimentu - tříbodovým ohybem na trámci s centrálním zářezem, viz obr. 1.
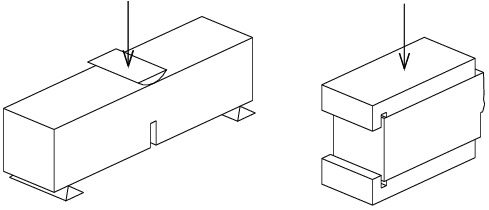
Obrázek 1: Schematické znázornění zatěžovacích zkoušek (vlevo tříbodový ohyb trámce se zářezem a vpravo tlak na zlomku trámce)
Jednou z jednodušších možností jak tuto souvislost odhalit je získání relevantních zatěžovacích diagramů pomocí numerického modelování. Tento příspěvek se týká numerického modelování zatěžovací zkoušky tlakem na zlomku vzorku/trámečku získaného ze zkoušky v tříbodovém ohybu, viz obr. 1 vpravo.
Vzhledem k relativní složitosti porozumění porušení kvazikřehkého vzorku tlakem je třeba se zmínit o důležitých aspektech, které jsou známé z provedených experimentů. Vzorek tvaru kvádru se čtvercovým průřezem (obr. 2), se v experimentech porušoval většinou tak, že po dosažení mezního stlačení zůstaly soudržné pouze dva klínovité útvary přiléhající k tlačeným plochám,
viz obr. 2.

Obrázek 2: Schematické znázornění klínovitých útvarů zbylých po zatěžovací zkoušce
Tento fakt nám při zjednodušení umožňuje chápat způsob porušování vzorku jako konstantní po délce kvádru. Zajímavý je rovněž proces iniciace trhlin, problém vystižení ztráty stability bočních stěn a zachovávání symetrie porušení vzorku podle dvou vzájemně kolmých rovin (viz obr. 2) i při reálné proměnlivosti vlastností vzorku.
2 Model, parametry
Pro modelování zatěžovací zkoušky tlakem na zlomcích trámečků byla vybrána metoda konečných prvků, pro hledání statických nelineárních řešení implementovaná v programu ATENA 2D [1]. Vzorek reprezentují stěnové konečné prvky neproměnných vlastností s fyzikálně nelineárním modelem betonu SBETA. Úloha je zjednodušeně uvažována jako rovinná napjatost (důsledky tohoto možná výrazného zjednodušení budou zvlášť analyzovány na trojrozměrném MKP modelu v programu ATENA 3D).
Při vytváření 2D modelu se v souladu s výsledky experimentů uvažuje, jak již bylo zmíněno, že se průběh porušení nemění podél nejdelší strany vzorku. Tato strana je tedy ve stěnovém modelu MKP nahrazena tloušťkou konečných prvků.
Vzhledem k nejistotám v chování kontaktu mezi ocelovými přípravky a testovaným vzorkem se uvažují dva extrémy interakce na tomto rozhraní. Samotné přípravky jsou vzaty jako absolutně tuhé (v modelu je reprezentují nepoddajné vazby). Prvním případem, který nazveme "tuhý kontakt", je úplné zamezení tangenciálního posuvu (smýkání) na kontaktních plochách, viz obr. 3a. Druhý případem, který nazveme "volný kontakt", viz obr. 3b, je úplná volnost tangenciálního pohybu vzorku. Předmětem zkoumání je tak vliv těchto extrémně odlišných okrajových podmínek na výsledky zatěžovací zkoušky a na stabilitu a způsob porušení modelu.
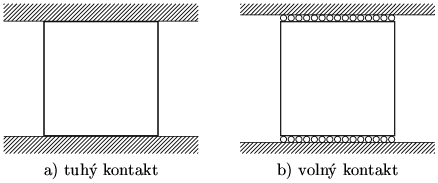
Obrázek 3: Dva extrémní případy okrajových podmínek modelu
Již bylo řečeno, že úloha je pojata zjednodušeně jako rovinná napjatost a chování materiálu je aproximováno fyzikálně i geometricky nelineárním materiálovým modelem SBETA, přičemž je uvažováno exponenciální tahové změkčení, rotovaný model rozetřených trhlin, lineární interakce tahu a tlaku a "CrushBand" tlakové změkčení. Zvolen je konečný prvek čtyřúhelníkový označený "CCIsoQuad". Hodnoty rozhodujících parametrů modelu (stanovené přibližně z provedených experimentů) jsou následující: šířka a výška vzorku 4 cm, tlošťka konečných prvků 8 cm, modul pružnosti E = 35.8 GPa, Poissonovo číslo 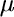 = 0.2, pevnost v tahu Rt = 3.3 MPa, pevnost v tlaku Rc = -36.3 MPa, specifická lomová energie Gf = 6 N/m.
= 0.2, pevnost v tahu Rt = 3.3 MPa, pevnost v tlaku Rc = -36.3 MPa, specifická lomová energie Gf = 6 N/m.
Poznamenejme, že hodnoty parametrů v prvním přiblížení nemusejí přesně vystihovat chování použitého reálného materiálu, jelikož jde zejména o porovnání vlivu okrajových podmínek a test numerického modelu.
3 Výpočet
Reálné zatěžování vzorků probíhá s konstantním přírůstkem deformace ve směru působícího zatížení a měří se potřebná síla k udržení klidového rovnovážného stavu. Zaznamenáním těchto veličin se získá zatěžovací diagram síla-průhyb, tzv. l-d diagram. V programu ATENA lze zatěžování konstantním přírůstkem deformace snadno realizovat. Přírůstek deformace je nastaven na 0.01 mm.
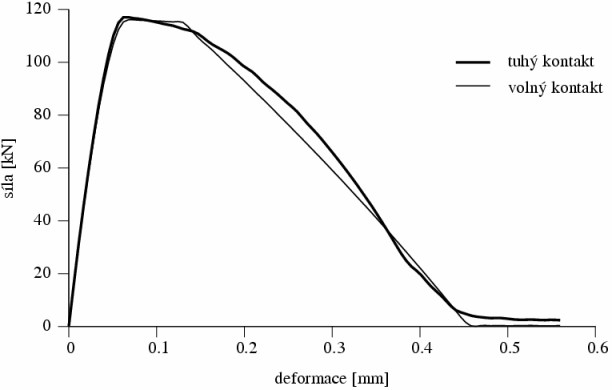
Na obr. 4 jsou vidět vypočtené zatěžovací l-d diagramy pro oba extrémní případy okrajových podmínek na modelu s 16 (čtvercovými) konečnými prvky na každé straně průřezu vzorku (celkem tedy 256 prvků). Z grafu je patrné, že ačkoliv je průběh obou funkcí mimo jejich vzestupnou část výrazně odlišný, tak se vykonaná přetvárná práce o mnoho neliší. Jiná je situace u modelu s 32 prvky na každé straně vzorku (celkem 1024 prvků, obr. 5). Zatěžovací diagram pro tuhý kontakt je ve velmi dobré shodě s modelem 16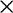 16 prvků, ovšem diagram pro volný kontakt se zásadně odlišuje, viz obr. 5. Rozdíly mezi porušením modelu s tuhým a volným kontaktem a důvody odlišnosti výsledku výpočtu u modelů s volným kontaktem při různém dělení jsou dobře patrné ze sledování rozvoje "trhlin".
16 prvků, ovšem diagram pro volný kontakt se zásadně odlišuje, viz obr. 5. Rozdíly mezi porušením modelu s tuhým a volným kontaktem a důvody odlišnosti výsledku výpočtu u modelů s volným kontaktem při různém dělení jsou dobře patrné ze sledování rozvoje "trhlin".
Obrázek 4: Zatěžovací l-d diagram získaný výpočtem modelu s 16 16-ti konečnými prvky
16-ti konečnými prvky
Obrázek 5: Zatěžovací l-d diagram získaný výpočtem modelu s 32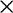 32-ma konečnými prvky
32-ma konečnými prvky
V případě tuhého kontaktu se chování modelů s různým dělením kvalitativně neliší. Způsob průběhu porušení je znázorněn na obr. 6. Situaci lze popsat následovně: Nejprve dochází k porušení v oblasti rohů vzorku vlivem koncentrace namáhání (zejména styku), viz obr. 6a. Díky smyku dojde k vytlačení bočních částí vzorku, což má za následek vytvoření výsledných klínovitých útvarů, viz obr. 6b.
 | 
|
| a) první porušení (stlačení 0.05 mm) | b) rozvinutí klínových útvarů (stlačení 0.08 mm) |
Obrázek 6: Dva rozhodující okamžiky zatěžování modelu 32 32 prvků s tuhým kontaktem (trhliny zobrazeny černou barvou, síť prvků šedou barvou)
32 prvků s tuhým kontaktem (trhliny zobrazeny černou barvou, síť prvků šedou barvou)
Volný kontakt je z hlediska numerického výpočtu programem ATENA 2D problematický. Oba modely se shodují v počátečním porušení, kdy vznikají "sloupce" příčným tahem porušených prvků, viz obr. 7, obr. 8a. Kvalitativní odlišnosti se objeví při dosažení určitého kritického bodu, který odpovídá počátku sestupné větve zatěžovacího diagramu (obr. 4 a obr. 5). U modelu
16 16 prvků je kritickým okamžikem deformace 0.14 mm, kdy dojde k drcení první horní řady prvků modelu, viz obr. 4 (patrné pouze jako snížení výšky vrstvy).
16 prvků je kritickým okamžikem deformace 0.14 mm, kdy dojde k drcení první horní řady prvků modelu, viz obr. 4 (patrné pouze jako snížení výšky vrstvy).

Obrázek 7: Dosažení kritického bodu u modelu 16 16 prvků s volným kontaktem (stlačení 0.14 mm)
16 prvků s volným kontaktem (stlačení 0.14 mm)
Při výpočtu modelu s 32 32-ma prvky bylo dosaženo kritického bodu až při deformaci asi 0.3 mm, kdy došlo ke ztrátě stability celého vzorku, viz obr. 8.
32-ma prvky bylo dosaženo kritického bodu až při deformaci asi 0.3 mm, kdy došlo ke ztrátě stability celého vzorku, viz obr. 8.
 | 
|
| a) první porušení (stlačení 0.07 mm) | b) ztráta stability (stlačení 0.33 mm) |
Obrázek 8: Dva rozhodující okamžiky zatěžování modelu 32 32 prvků s volným kontaktem
32 prvků s volným kontaktem
4 Závěr
Provedené numerické výpočty naznačují, že úloha tlačeného vzorku z kvazikřehkého materiálu je poměrně náročná. Výpočet se obzvlášť v případě volného kontaktu zřejmě neobejde bez geometricky nelineární formulace, jelikož dochází ke ztrátě stability částí vzorku.
Z hlediska výpočetní stability a také při porovnání s výsledky experimentů se jeví výstižnější případ tuhého kontaktu vzorku s ocelovými přípravky. Vzniklé klínovité útvary dobře souhlasí s útvary vzniklými při experimentu.
Vzhledem k tomu, že úloha je silně nelineární a zřejmě existuje více řešení, jak naznačují výsledky výpočtu modelu s volným kontaktem, bude zapotřebí podrobnější studie v okolí kritického bodu při počátku sestupné větve zatěžovacího diagramu.
Poděkování
Práce na příspěvku byly podporovány z prostředků projektů MŠMT 1K041111 a GA ČR 103/03/1350.
Literatura
[1] ČERVENKA, V. and PUKL, R.: ATENA - Theory and Users manual for ATENA 2D, Červenka Consulting, Praha: 2003